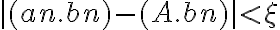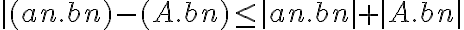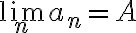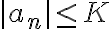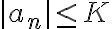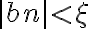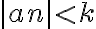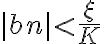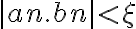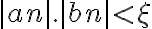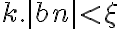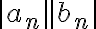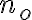Foro Práctico 3

Hola, me gustaría que me dijeran si está correcta la demostración que hice para este ejercicio. Si hay algun error, ¿Podrían ayudarme a corregirlo y reordenarlo? 

La letra dice lo siguiente:

demostración: 

tomo un $\xi$ cualquiera

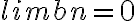
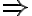
por hipótesis como 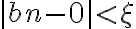$limbn=0$ $\Rightarrow$ $|bn - 0|< \xi$ , también pasa lo mismo con 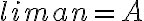$lim an=A$ que queda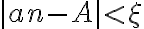 $|an-A|< \xi$

entonces limite de an.limite de bn = 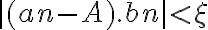$|(an-A).bn|< \xi$

$\Rightarrow$

$|(an.bn)-(A.bn)|< \xi$

$\Rightarrow$ por desigualdad triangular

$|(an.bn)-(A.bn) \leq|an.bn| + |A.bn|$ 

ahora, si usamos la hipótesis, sabemos que el limite de bn tiende a 0, por lo tanto 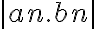$|an.bn|$ tiende a 0, por ser 0 x acotado y 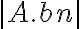$|A.bn|$ también es 0, ya que A es un numero natural y bn tiende a 0.

¿Es correcto? Aguardo respuesta, gracias.