Buenas, mi duda es acerca de la parte b del ejercicio, no se me ocurre como demostrar a a partir de que la sucesión no este acotada el límite diverge. Es equivalente si demuestro que si diverge seguro la sucesión no esta acotada?.
En respuesta a Gonzalo Nahuel Gimenez Cuello
Re: Ejercicio 4 de la parte COMPLEMENTARIOS
de Bernardo Marenco -
Hola. Ojo que lo que no está acotado es la función 
. La idea es probar que, sabiendo que no está acotada, construyas una sucersión 
tal que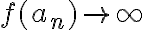 
. En la parte a) te piden escribir la negación de acotación de una función, es decir, la definición de que una función no esté acotada. La idea es usar esa definición para construir la sucesión buscada.
Saludos