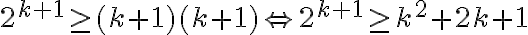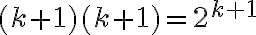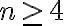Buenas. Disculpas por la respuesta tardía, pero a lo mejor sigue ayudando.
Hay varias detalles.
Primero, separar en partes de paso base y paso inductivo. Indicar claramente que estás usando P(4) como tu paso base. Y antes de plantear la HI y la TI indicar que eso es el paso inductivo.
Cuando reescribis la tesis inductiva queda bastante confuso con símbolos . Lo correcto es usar
. Lo correcto es usar 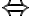 , es decir:
, es decir:
Hay varias detalles.
Primero, separar en partes de paso base y paso inductivo. Indicar claramente que estás usando P(4) como tu paso base. Y antes de plantear la HI y la TI indicar que eso es el paso inductivo.
Cuando reescribis la tesis inductiva queda bastante confuso con símbolos
 . Lo correcto es usar
. Lo correcto es usar  , es decir:
, es decir:Después, lo que dijiste no alcanza para probar 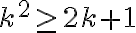 . Eso se prueba por ejemplo por inducción también (de hecho el ejercicio anterior consiste en probar eso, así que si ya lo hiciste podés decir que se cumple por ese ejercicio simplemente).
. Eso se prueba por ejemplo por inducción también (de hecho el ejercicio anterior consiste en probar eso, así que si ya lo hiciste podés decir que se cumple por ese ejercicio simplemente).
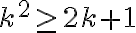 . Eso se prueba por ejemplo por inducción también (de hecho el ejercicio anterior consiste en probar eso, así que si ya lo hiciste podés decir que se cumple por ese ejercicio simplemente).
. Eso se prueba por ejemplo por inducción también (de hecho el ejercicio anterior consiste en probar eso, así que si ya lo hiciste podés decir que se cumple por ese ejercicio simplemente).