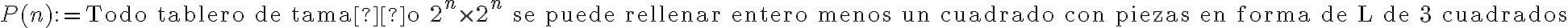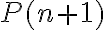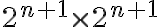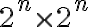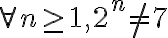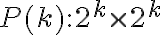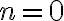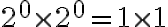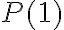Práctico 1 - Ejercicio 9

Práctico 1 - Ejercicio 9

de César Manuel Rodriguez Pereira -
Número de respuestas: 8

Buenas, tengo una duda, para demostrar que puedo llenar de L de 3 cuadraditos una condición es que los cuadrados restantes de sacarle 1 debe ser múltiplo de 3, es decir 2^2n-1=múltiplo de 3, esa condición se cumple, pero cómo puedo demostrar que puedo llenar el cuadro en todas las posiciones posibles? Gracias!

Ejercicio

En respuesta a César Manuel Rodriguez Pereira

Práctico 1 - Ejercicio 9

de Gabriel Mello -
Hola César.

Si bien es cierto que una condición necesaria para que se pueda llenar con L's es que la cantidad de cuadraditos por rellenar sea múltiplo de 3, es claro que no es suficiente (basta considerar una situación donde te quede una línea de 3 sin rellenar). La clave está en como decís, pensar cómo podemos hacer para que se pueda en cualquier posición. Para esto es muy importante prestar atención a cuál es nuestra hipótesis inductiva y nuestra tesis inductiva, y por ende la definición de la propiedad (que nunca especificaste quién es). 
 
Podemos definir la propiedad como P(n) := \text{Todo tablero de tamaño } 2^n \times 2^n \text{ se puede rellenar entero menos un cuadrado con piezas en forma de L de 3 cuadrados} , para cada n fijo. Luego, nuestra hipótesis inductiva es P(n) y nuestra tesis inductiva es  P(n+1) . 
 
La idea para demostrar el paso inductivo es la siguiente: 
  1. Tomemos un tablero de tamaño 2^{n+1} \times 2^{n+1} y dibujemos la línea vertical y horizontal que pasan por su centro, obteniendo 4 tableros de tamaño 2^n \times 2^n . 
  2. Por definición de la propiedad, al tablero grande lo queremos rellenar todo salvo un cuadradito, que va a tener que estar en alguno de los 4 tableros más chicos. 
  3. A ese que le falta un cuadradito, lo sabemos rellenar por hipótesis inductiva (ya que es del tamaño que indica P(n) ). 
  4. A los otros 3, los sabríamos rellenar si ya cada uno de ellos tuviera un cuadradito rellenado. Para conseguir esto, ponemos una pieza en forma de L que cubra cada una de las esquinas de esos 3 tableros chicos que están en el centro del tablero grande (ver imagen) y luego sabemos rellenar el resto por hipótesis inductiva.

Tablero

Otros comentarios:

  • El ejemplo que dibujaste de un tablero 7x7 no cumple con las condiciones del problema, ya que \forall n \geq 1, 2^n \neq 7
  • Todo esto que te acabo de comentar sobre cómo construir la solución a este problema específico es una excusa para tener un ejercicio donde puedan ver cómo se usa el principio de inducción para demostrar cosas que no sean exclusivamente aritméticas. Lo más importante del ejercicio es ser capaz de estructurar correctamente la demostración usando el principio de inducción completa. Para esto te propongo que leas detenidamente mi respuesta a la pregunta que hicieron más abajo sobre el ejercicio 7. Una vez que hayas terminado de reescribir tu demostración podés volver a subirlo como respuesta a este mismo hilo y te lo vuelvo a revisar.

Ante cualquier duda que te haya quedado o comentario que quieras hacer no dudes en volver a escribir.

Saludos,

Gabriel
En respuesta a Gabriel Mello

Práctico 1 - Ejercicio 9

de César Manuel Rodriguez Pereira -

Solución Solución

En respuesta a César Manuel Rodriguez Pereira

Práctico 1 - Ejercicio 9

de Gabriel Mello -
Eso que mandaste ahora es una demostración correcta del paso inductivo. No obstante, una demostración por inducción consta de 4 partes:
  1. Identificación de la propiedad
  2. Paso base
  3. Paso inductivo
  4. Conclusión

Para terminar el ejercicio, te invito a que escribas las 4 partes y mandes foto de todas.

En respuesta a Gabriel Mello

Re: Práctico 1 - Ejercicio 9

de Agustina Arsuaga Maestri -

Hola, cómo estás? Quería saber si mi ejercicio está correcto.

En respuesta a Agustina Arsuaga Maestri

Re: Práctico 1 - Ejercicio 9

de Gabriel Mello -
Hola Agustina.

Primero que nada hago una aclaración sobre mi respuesta de 2023. Cuando digo en la definición de la propiedad "para cada n fijo", me refiero a que dado n se define P(n) como "Todo tablero (...) forma de L". Es decir, la parte del para todo no es parte de la definición de la propiedad, si no no tendría sentido.

En tu desarrollo decís que S es vacío, lo cual no sólo es falso si no que contradice lo que decís a continuación. Supongo que te comiste el "no" en "no vacío" pero lo resalto por las dudas.

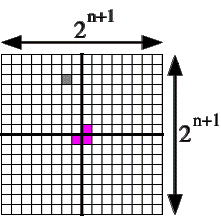
No se entiende qué es lo que quisiste decir con el dibujo del paso base. Lo que dibujaste en color queda por fuera del tablero 2x2. La forma de colocar la pieza en forma de L es tal que quede sobre los cuadraditos 1, 2 y 3, y esta es la única que funciona en el paso base.

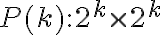
A lo largo de todo el desarrollo escribís cosas como P(k) : 2^k \times 2^k . Tampoco se entiende a qué te referís con eso. La proposición es exactamente la que definiste al principio del ejercicio, no es un número ni una igualdad. Esa cantidad que escribís es solamente el tamaño del tablero sobre el cual se hace la afirmación, no la afirmación en sí.

En la demostración del paso inductivo observás correctamente que el tablero se puede separar en 4 subtableros que satisfacen la hipótesis inductiva pero no deducís nada de ello.

En mi respuesta de hace un par de años en este mismo hilo ya hice mi mejor esfuerzo por explicar cómo demostrar el paso inductivo, así que si ya lo leíste (cosa que estoy asumiendo porque definiste la proposición como yo ahí) y no lo entendiste te recomiendo que vayas a alguna clase de práctico ya sea presencial o virtual para que alguno de los docentes te pueda explicar de forma síncrona hasta resolverte las dudas.

Saludos,
Gabriel
En respuesta a Gabriel Mello

Re: Práctico 1 - Ejercicio 9

de Florencia Maria Trinidad Vila -
hola, quisiera saber si la forma de la que resolvi este ejercicio es la correcta. abri una entrada en el foro el 14 de marzo y no tuve respuesta aun.
ej 9 pract 1
 
En respuesta a Florencia Maria Trinidad Vila

Re: Práctico 1 - Ejercicio 9

de Gabriel Mello -
Hola Florencia.

El primer error es que nunca definiste explícitamente quién es la proposición abierta P(n) a la cual le vas a aplicar el principio de inducción. Esto lleva a que cuando enunciás la hipótesis inductiva digas "el tablero" como si fuera uno dado y no "cualquier tablero" que es lo correcto en este caso, cosa que usás fuertemente en tu demostración del paso inductivo.

Otra observación es que si bien la letra dice explícitamente que el tablero debe ser al menos de 2x2, no es cierto que para n =0 no exista un tablero del tamaño correspondiente. Un tablero de tamaño 2^0 \times 2^0 = 1 \times 1 es simplemente un tablero compuesto por un solo cuadradito. Más aún si a ese tablero le sacamos un cuadradito, no queda nada por cubrir por lo que efectivamente se puede cubrir entero con piezas en forma de L (se necesitan 0 piezas). Elegimos imponer la condición de que sea de al menos 2x2 para que no tuvieran que pensar ese caso borde, pero funciona sin problemas.

No enunciaste qué es lo que vas a probar en el paso base, es decir su tesis. Si hubieras definido la propiedad esto habría sido tan fácil como decir que la tesis era P(1) .

Cuando enunciaste tu hipótesis y tesis inductivas no dijiste antes que estabas enunciando el paso inductivo.

En tu demostración del paso inductivo decís que de los 3 tableros a los que no les falta un cuadradito se les puede sacar en forma de L. Dado que hay una única forma de hacer esto (que es la que mostré con la imagen que adjunté más arriba en mi respuesta de 2023) sería bueno que explicaras cómo es que se hace. Para no tener que escribir un párrafo entero es válido un dibujo ilustrativo.

En la conclusión corresponde aclarar que la propiedad es verdadera para todos los naturales mayores o iguales a 1 y que esto se deduce por aplicación del PIC porque verificaste sus hipótesis, es decir el paso base y el paso inductivo. Esto podría quedar así por ejemplo: Por lo probado en el paso base, el paso inductivo, y aplicando el PIC tenemos que \forall n \geq 1, P(n)
 
Saludos,
Gabriel