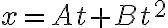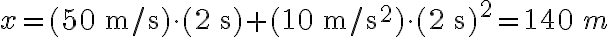No comprendo el uso de la ecuacion ene l problema, y tampoco entiendo si los valores que nos dan en A y B son solo de la ecuacion o se pueden interpretar como la velocidad y aceleracion de la particula?
En respuesta a Ignacio Kononovas Arigón
Re: Practico 2 ejercicio 3
Todo bien Ignacio?
Yo lo resolví derivando esa ecuación de posición. La velocidad te queda 2Bt + A ( de ahí sacás que A = 50m/s es la velocidad inicial), y derivando la velocidad te queda la aceleración (2B) que es 20 m/s en todo tiempo porque es constante.
Abrazo
Yo lo resolví derivando esa ecuación de posición. La velocidad te queda 2Bt + A ( de ahí sacás que A = 50m/s es la velocidad inicial), y derivando la velocidad te queda la aceleración (2B) que es 20 m/s en todo tiempo porque es constante.
Abrazo
Hola, Ignacio. Te recomiendo que repases el capítulo 2 del libro, y en partícular fíjate en los ejemplos que aparecen en la sección 2-2. Después del repaso, trata de hacer nuevamente este ejercicio y creo que va a quedar más claro lo que se pide.
En el ejercicio 3, te dicen que una partícula se mueve de forma que su coordenada en el eje cumple la ecuación
Las letras 
y 
representan constantes, cuyos valores te indica el ejercicio, y 
es el tiempo (en segundos). El tiempo se considera la variable independiente. Para cualquier valor de tiempo, la ecuación permite calcular la posición. Por ejemplo, si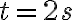 
, entonces sustituimos todos los valores conocidos y planteamos
.
Esa es la posición del cuerpo en el eje de coordenadas cuando el tiempo es 2 s, y se puede hacer en forma análoga para cualquier otro valor del tiempo .
Se te pide hallar la velocidad y la aceleración instantáneas a partir de la información dada. Para ello, utiliza la definición de estas cantidades (repasa las secciones 2-4 y 2-5 del libro). El resultado depende del movimiento del cuerpo dado por su coordenada x, así que hay que usar las constantes y para hacer el cálculo.
Suerte,
NC