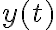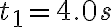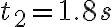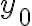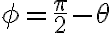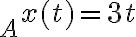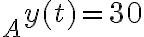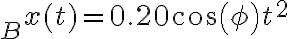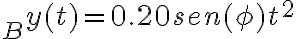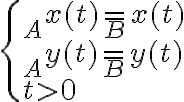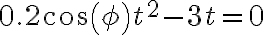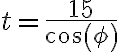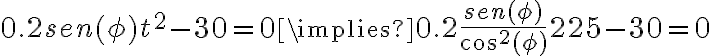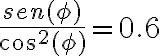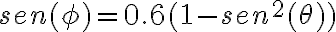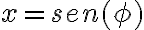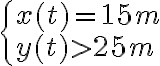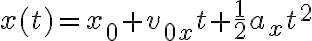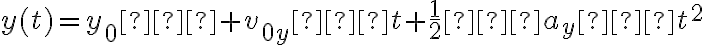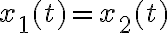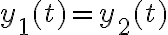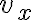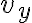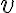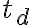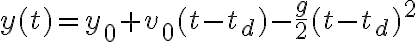Buen día.
Hoy Jueves, asistí al teórico de Nicolás Casaballe, y al práctico de Stari.
Aun así,
- El ejercicio 6 agregado tardíamente al repartido (fomenta la confusión el hacer esas cosas), me resulta en 78,4m la altura 1, y la segunda altura 15,9m. No encuentro forma de saber si está bien lo que hice.
- No encuentro una resolución al ejercicio 9 de colisiones entre partículas, pienso que es más sencillo de lo que parece, y aún así no obtengo resultado numérico.
- No sé qué aplicar ni tengo la resolución de la parte c) del ejercicio 10 que pregunta si la partícula supera la pared. Agradezco ver la resolución, para entender un poco mejor.
- Ni que hablar de los ejercicios 11 y 12: no llegué.
Consulto a ver si pueden facilitar las resoluciones explicadas, o al menos de los últimos ejercicios que son los que como modelo van para los parciales.
Y otras dos cosas:
- No sé por qué hacen alarde de que saben resolver un ejercicio o explicar un teórico, cuando en realidad me mareo más con la sensación ambiente de inseguridad que se transmite, seguro a ustedes no les enseñaron de esa forma, y si fue así, con razón son pocos los que quedan.
- Por favor, no se tomen esto personal, es una cuestión de estudio, como si fuera trabajo. Me refiero a que si alguien les pregunta algo en concreto, eso es lo que tienen que responder como Profesores, y no "una guía de qué pensar" o un "rezongo". Recibí correos de intercambios entre ustedes y compañeros, por el foro, al respecto.
Gracias.
Saludos.
Valentina Andriulis Candia.