Buenas! Espero se encuentren bien.
Una consulta. Si para un código coinciden su matriz de chequeo de paridad y su matriz generatriz entonces es dual a sí mismo?
Si lo anterior es verdad, en este siguiente caso, si vemos que las matrices coinciden a menos de reorganizar las columnas ya es suficiente para decir que es dual a si mismo? O hace falta hacer toda la escalerización para poder afirmar realmente que el código es dual a sí mismo?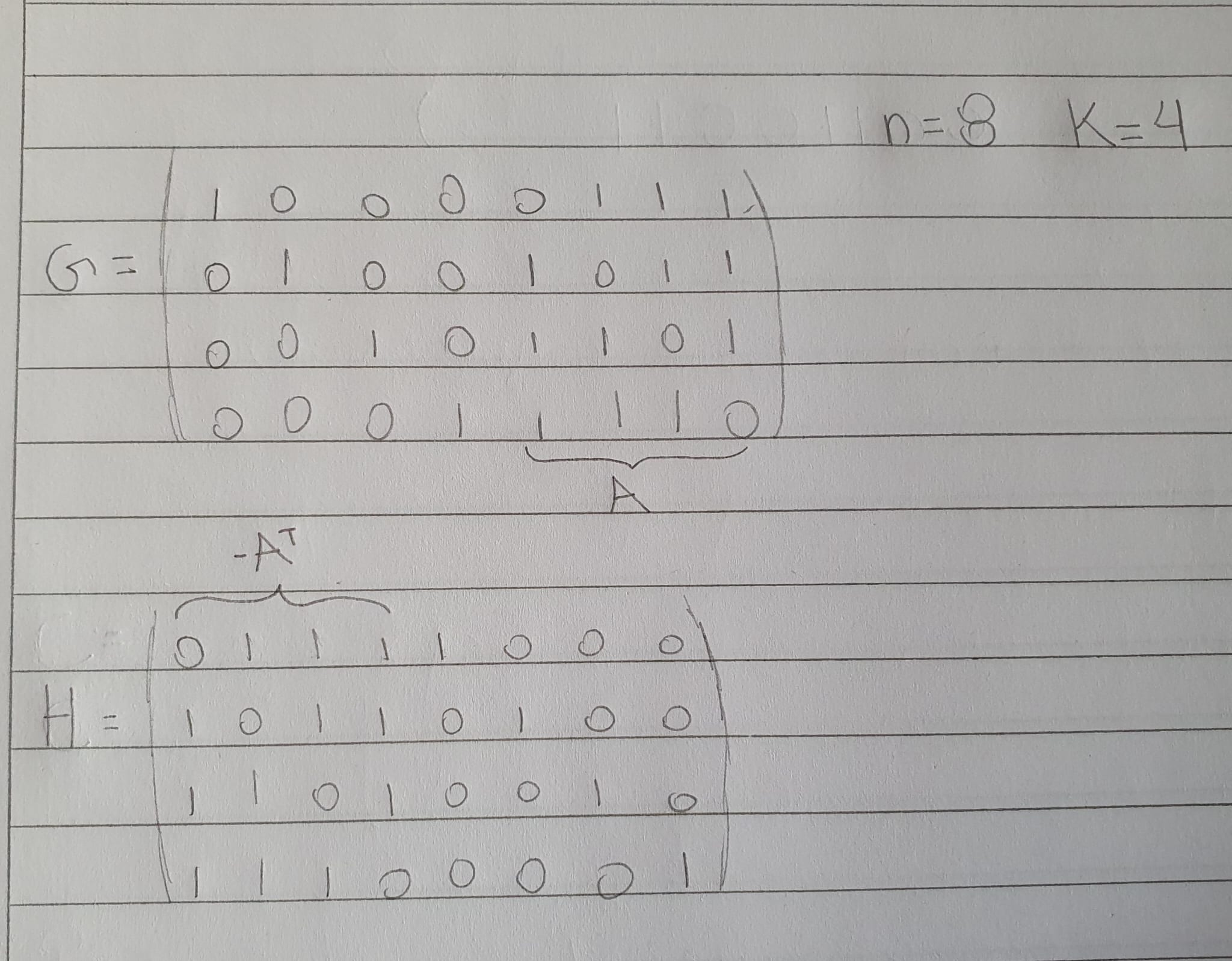
Muchas gracias!
Saludos,
Diego Furrer
Muy buena pregunta. Si las matrices coinciden exactamente, el código es dual a sí mismo. De hecho, el tema de "self-dual codes" es muy estudiado en teoría de códigos. En principio, no alcanza con que H sea una permutación de las columnas de G. Hay más de una manera de demostrar que un código es auto-dual. Una es como decís, transformando G y/o H hasta que sean iguales. Otra es tomar una de ellas y demostrar que es ortogonal a sí misma (luego de verificar que las dimensiones y rangos cuadran).
--Gadiel
Excelente, muchas gracias! Saludos
