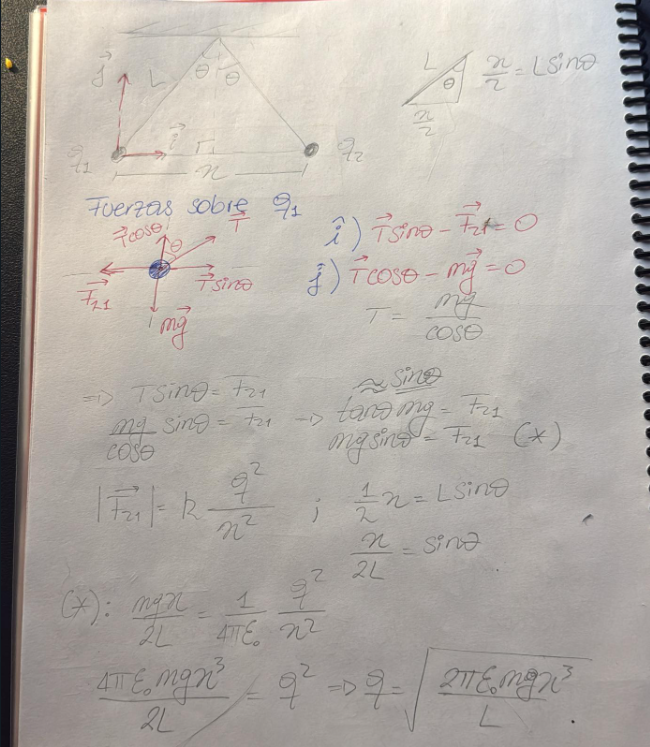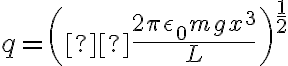Buenas! Te comento cómo lo resolví yo, capaz logras entender mejor.
En el versor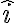 tengo las mismas ecuaciones que vos, es decir,
tengo las mismas ecuaciones que vos, es decir, 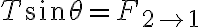 y en
y en 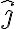 también lo mismo (
también lo mismo (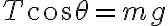 )
)
Traté de despejar la tensión de la ecuación en el versor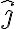 tal que
tal que 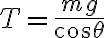 y luego usé ese valor de
y luego usé ese valor de 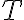 en la ecuación de
en la ecuación de 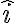 , quedándome:
, quedándome:
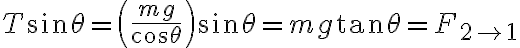 , es decir,
, es decir, 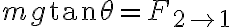 pero por letra (creo que es pequeñas oscilaciones) sabés que
pero por letra (creo que es pequeñas oscilaciones) sabés que 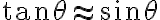 entonces tenés
entonces tenés 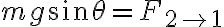
En el versor
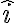 tengo las mismas ecuaciones que vos, es decir,
tengo las mismas ecuaciones que vos, es decir, 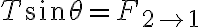 y en
y en 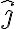 también lo mismo (
también lo mismo (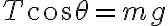 )
)Traté de despejar la tensión de la ecuación en el versor
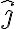 tal que
tal que 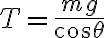 y luego usé ese valor de
y luego usé ese valor de 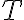 en la ecuación de
en la ecuación de 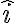 , quedándome:
, quedándome: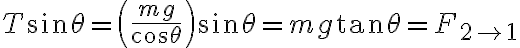 , es decir,
, es decir, 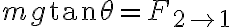 pero por letra (creo que es pequeñas oscilaciones) sabés que
pero por letra (creo que es pequeñas oscilaciones) sabés que 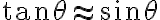 entonces tenés
entonces tenés 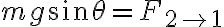
Los dos despejamos a 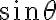 como
como 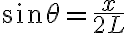 así que nos quedaría
así que nos quedaría 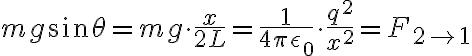 (por las dudas escribí a la fuerza eléctrica que hace la carga 2 sobre la carga 1 como
(por las dudas escribí a la fuerza eléctrica que hace la carga 2 sobre la carga 1 como 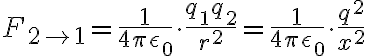 )
)
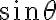 como
como 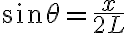 así que nos quedaría
así que nos quedaría 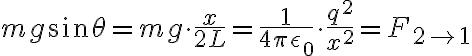 (por las dudas escribí a la fuerza eléctrica que hace la carga 2 sobre la carga 1 como
(por las dudas escribí a la fuerza eléctrica que hace la carga 2 sobre la carga 1 como 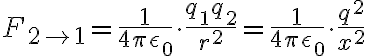 )
)(paso foto del planteo por si no queda del todo claro)