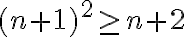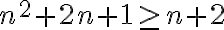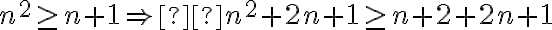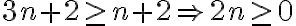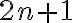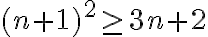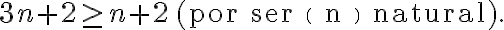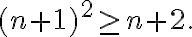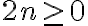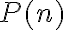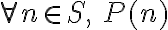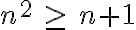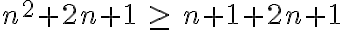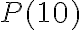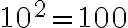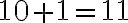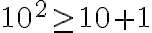Intenté hacerlo lo más completo posible, aunque deduzco que tengo problemas de estructuración, ¿así estaría bien?
Resolución Ejemplo #4 Práctico 1
1. Probaremos que para todo entero n tal que n≥10 se cumple que:
P(n) = n² ≥ n+1, ∀n∈N; n≥10
2. Paso Base: Demostrar que P(n) se cumple el primer valor de n para el que queremos que se cumpla, es decir, n=10.
P(10): Sustituir n=10
10² ≥ 10+1
100 ≥ 11
Se cumple, por tanto, P(n) es válida para el menor valor de n posible.
• Paso Inductivo: Probaremos que ∀n∈N; n≥10, P(n) ⇒ P(n+1)
• Hipótesis Inductiva: P(n)
n² ≥ n+1
• Tesis Inductiva: P(n+1)
(n+1) ² ≥ (n+1) +1
• Demostración del Paso Inductivo:
(n+1) ² ≥ n+2
n²+2n+1≥ n+2
Asumiendo que n² ≥ n+1 por la Hipótesis Inductiva, entonces sustituimos a n² en la desigualdad:
n²+2n+1≥ n+2 ⇒ n+1+2n+1≥ n+2 ⇒ 3n+2≥ n+2 ⇒
3n+2−n−2 = 2n≥0
Se cumple porque n∈N, por tanto la desigualdad se satisface ∀n∈N.
Como probamos que el Paso Base P(10) y el Paso Inductivo P(n+1) se cumplen. Concluimos por el principio de Inducción Completa que:
∀n∈N; n≥10, P(n).
Pd: Aún no sé como escribir fórmulas matemáticas acá.
(Editado por Pablo Romero - envío original lunes, 10 de marzo de 2025, 00:52)

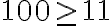
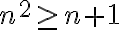
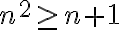 a que
a que