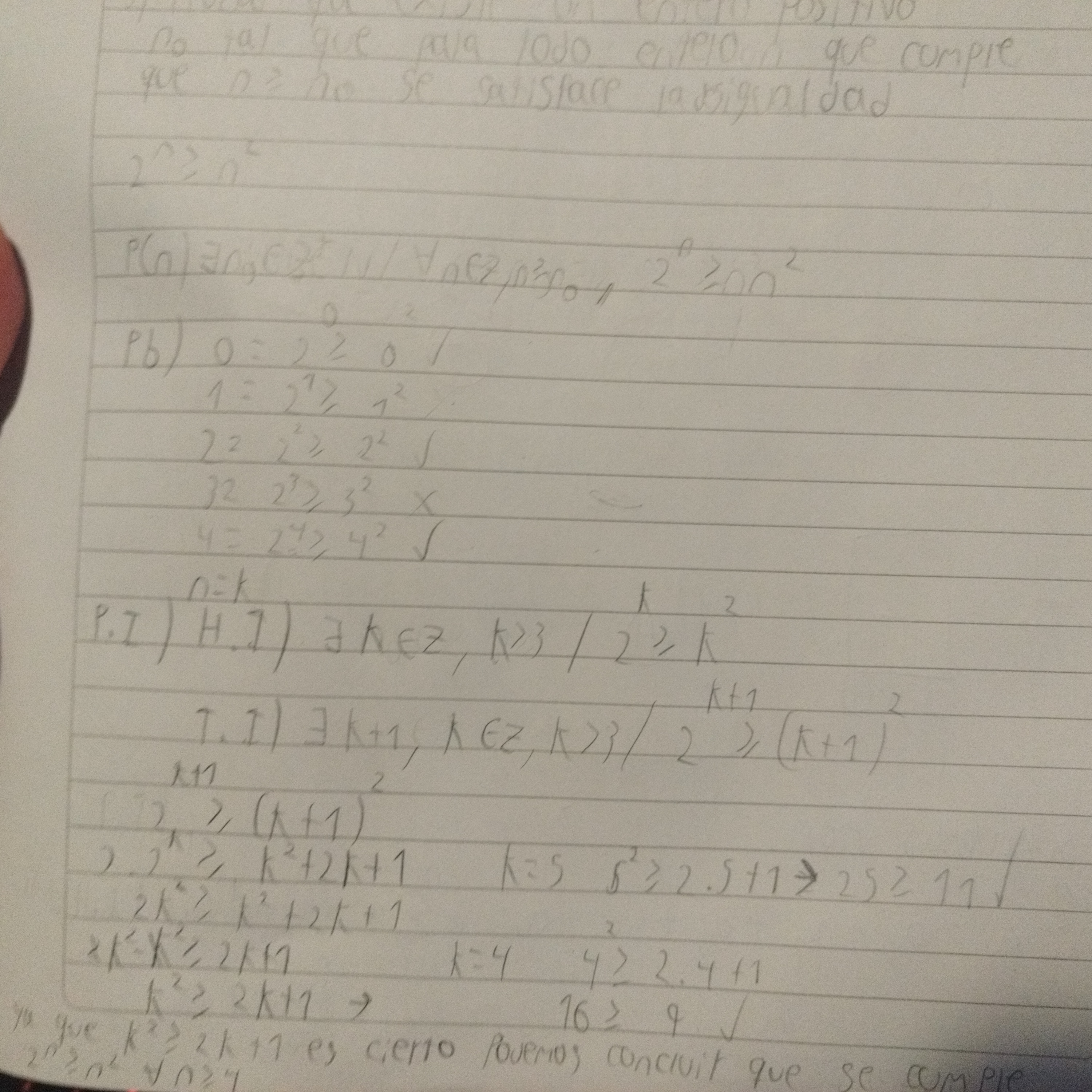En este ejercicio hay que encontrar el n0 para seguir con el paso base a partir de este, ¿se puede hacer por prueba y error o hay algún método para encontrarlo?
Hola,
Depende a qué le llamemos método. Un algoritmo que funcione automáticamente no, porque puede ser que aparezcan valores de n para los que la propiedad sea cierta, pero que no sirvan como base inductiva. En el ejemplo que mencionas, para n=0 la propiedad se satisface, pero no es cierta para todos los naturales (esto lo afirmo porque ya lo hice).
Mi sugerencia general de algo que se parece a un algoritmo (que lo tiene que "pilotar" quien lo esté aplicando) es que intentes primero probar el paso inductivo y te fijes para qué naturales tu prueba funciona. Por ejemplo, si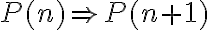
para todo 
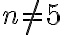, eso significa que con la prueba que hallaste para el paso inductivo, la propiedad se puede probar por inducción sólamente a partir de 
. Luego quedaría buscar el primer 
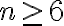que la cumpla (y ahí sí tantearía los naturales uno por uno) y a partir de ahí ya sabes que tienes una prueba por inducción. Siguiendo esta idea, en este ejemplo no necesitarás fatigarte mucho para encontrar tu base, pero es importante que mires con un ojo crítico tu prueba del paso inductivo.
Lo importante de ese ejercicio es que te quede claro que no necesariamente el primer natural que cumple una propiedad es una buena base inductiva, porque quizá el paso inductivo no funcione a partir de ahí. Su valor didáctico es exactamente ese.
Saludos cordiales,
MAURICIO.
Depende a qué le llamemos método. Un algoritmo que funcione automáticamente no, porque puede ser que aparezcan valores de n para los que la propiedad sea cierta, pero que no sirvan como base inductiva. En el ejemplo que mencionas, para n=0 la propiedad se satisface, pero no es cierta para todos los naturales (esto lo afirmo porque ya lo hice).
Mi sugerencia general de algo que se parece a un algoritmo (que lo tiene que "pilotar" quien lo esté aplicando) es que intentes primero probar el paso inductivo y te fijes para qué naturales tu prueba funciona. Por ejemplo, si
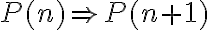para todo 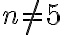, eso significa que con la prueba que hallaste para el paso inductivo, la propiedad se puede probar por inducción sólamente a partir de . Luego quedaría buscar el primer 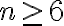que la cumpla (y ahí sí tantearía los naturales uno por uno) y a partir de ahí ya sabes que tienes una prueba por inducción. Siguiendo esta idea, en este ejemplo no necesitarás fatigarte mucho para encontrar tu base, pero es importante que mires con un ojo crítico tu prueba del paso inductivo.Lo importante de ese ejercicio es que te quede claro que no necesariamente el primer natural que cumple una propiedad es una buena base inductiva, porque quizá el paso inductivo no funcione a partir de ahí. Su valor didáctico es exactamente ese.
Saludos cordiales,
MAURICIO.
Muchas gracias Mauricio
Un gusto. ¡Buen trabajo!
MAURICIO.
MAURICIO.
Práctico 1 - Ejercicio 5:
Buen día. Era para consultar si está solución del ejercicio es correcta (la conclusión final está en el papel verde, porque no me daba el espacio).
Buenas David: la operatoria es correcta.
Tienes que explicar la reducción de tu demostración a otra que también empleará el principio de inducción completa.
Existen varias versiones de inducción tal como presentamos en clases de teórico. Debes ser explícito en el principio que estás utilizando, y sobre qué conjunto lo estás aplicando.
El uso del conectivo de "si y sólo si" no es correcto. Cuidado con dichas afirmaciones basadas en conectivos de tipo "si y sólo si", puesto que allí debes justificar que vale la doble implicancia, y ello requiere mayor justificación.
Por último, me pierdo con las notas que pones en amarillo. No sé en qué parte de la demostración se deben poner. Eso confunde la lectura.
Tienes que explicar la reducción de tu demostración a otra que también empleará el principio de inducción completa.
Existen varias versiones de inducción tal como presentamos en clases de teórico. Debes ser explícito en el principio que estás utilizando, y sobre qué conjunto lo estás aplicando.
El uso del conectivo de "si y sólo si" no es correcto. Cuidado con dichas afirmaciones basadas en conectivos de tipo "si y sólo si", puesto que allí debes justificar que vale la doble implicancia, y ello requiere mayor justificación.
Por último, me pierdo con las notas que pones en amarillo. No sé en qué parte de la demostración se deben poner. Eso confunde la lectura.
Recuerda que tu objetivo es comunicar lo más clara y efectivamente posible la demostración, de modo que cada paso sea avalado mediante tus hipótesis o tus resultados previos, y en lo posible que sea trivialmente verificable por un lector humano.
Cordiales saludos,
Pablo.
Buenas Pablo o alguno de los docentes encargados de corregir los ejercicios, quisiera que me dieras una corrección de errores o acotaciones sobre si lo que escribí en el ejercicio 5 cumple con la consigna de una inducción o no, y si no que le falta o sobra gracias.
Buenas Guillermo: identifico al menos 3 errores.
El primero es que defines mal la proposición abierta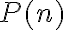
. Lo correcto era definir 
.
El primero es que defines mal la proposición abierta
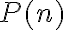. Lo correcto era definir .El segundo es que no enuncias el paso base sino que simplemente haces unas cuentas que ni siquiera explicas qué significan, lo que es un error bastante serio.
Es importante que no confundas verificar con hacer una demostración, que es lo que está ocurriendo aquí (donde aparentemente hacer un "tanteo" o verificación de si se cumplen o no algunas desigualdades, y luego te salteas el paso base y te diriges a explicar el paso inductivo).
El tercer error es que omites el dominio de la variable 
en el remate de la demostración.
Una vez que demuestres tanto el paso base para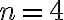
como el paso inductivo, vas a poder concluir que 
. En este caso el enunciado vale para todo número real tal que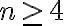 
, pero mediante el principio de inducción completa solamente puedes afirmar que 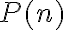es cierta para todo número natural tal que .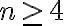
Cordiales saludos,
Pablo.
en el remate de la demostración. Una vez que demuestres tanto el paso base para
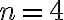como el paso inductivo, vas a poder concluir que . En este caso el enunciado vale para todo número real tal que 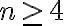, pero mediante el principio de inducción completa solamente puedes afirmar que 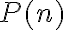es cierta para todo número natural tal que 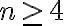.Cordiales saludos,
Pablo.
Buenas noches, quería consultar si me podrían corregir este ejercicio. Cualquier corrección es bienvenida
