Buenas, tenia una consulta sobre la parte c.
Una vez que hallamos g(x) que cumple x=g(x), para analizar su orden de convergencia alcanza con utilizar que x* ≈ 0.59, y entonces |g'(x*)| = 0.385 < 1? O esto es incorrecto/incompleto?
En respuesta a Nicolas Eduardo Navascues Soto
Re: [Examen Feb24] Ej 2.
En caso de que no sea suficiente y sea necesario hacer lo que se hace en la solución, no me doy cuenta como se llega a que x* pertenece a [0, pi/2].
Hola Nicolás,
El valor numérico aproximado de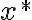
lo da la letra, así que podés usarlo libremente. Fijate que 
.
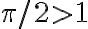La parte c) pide que plantees una iteración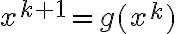
. En la solución pusimos una, pero en realidad hay infinitas opciones. El análisis del orden de convergencia va a depender de la función 
que hayas propuesto, pero lo que se hace en la solución es simplemente verificar que la que planteamos cumple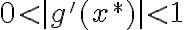 
y por lo tanto podemos asegurar que el método converge con primer orden.
El valor numérico aproximado de
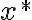lo da la letra, así que podés usarlo libremente. Fijate que 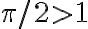.La parte c) pide que plantees una iteración
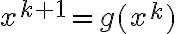. En la solución pusimos una, pero en realidad hay infinitas opciones. El análisis del orden de convergencia va a depender de la función que hayas propuesto, pero lo que se hace en la solución es simplemente verificar que la que planteamos cumple 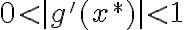y por lo tanto podemos asegurar que el método converge con primer orden.