Foro de Consultas de Evaluaciones Anteriores

Hola, Fabiana. Voy a intentar darte una mano, ya que hay varias cosas para considerar.

1) Fijate en el siguiente esquema que muestra el disco apoyado en el escalón. Marqué un vector que va desde el centro del disco hasta el punto de apoyo, junto con sus componentes horizontal y vertical. Uno de los pasos que puede resultar útil, según cómo se plantee el sistema, es hallar el tamaño de las componentes en función del radio del disco y la altura del escalón.

La componente vertical vale (en módulo) $r_y = R -h$. ¿Te animás a despejar el valor de $r_x$?

2) Hay una información clave en el ejercicio para saber la dirección de la fuerza que el escalón ejerce sobre el disco. El enunciado dice "La fuerza de contacto ejercida por las esquina del escalón sobre la rueda es radial". El hecho de que la fuerza sea radial significa que se puede dibujar aplicada en el punto de contacto y apuntando directamente hacia el centro de masa. El vector de esa fuerza tiene la dirección opuesta al vector 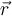$\vec r$ de antes. 

Debido a que los vectores tienen sentidos opuestos, el torque que esa fuerza ejerce con respecto al centro de masa es nulo. La condición de equilibrio para el torque neto con respecto al centro de masa queda entonces bastante sencilla. Sin embargo, también hay que plantear la fuerza neta sobre el disco, para lo cual conviene considerar las componentes horizontal y vertical de todas las fuerzas.

3) Pienso que en este ejercicio hay un factor de "shock" al darnos cuenta que la fuerza de rozamiento estática puede tener cualquier valor que cumpla $|\vec F_{roz}| \leq \mu_s |\vec N|$, incluyendo el caso $\vec F_{roz} = \vec 0$. Pero si las ecuaciones de equilibrio implican ese valor, entonces la conclusión es que la fuerza es nula, por más que nos sorprenda (análogamente para las demás fuerzas que puedan aparecer).

4) Para evaluar si el disco se mantiene en equilibrio o no, hay que determinar si es posible que se cumplan simultáneamente todas las condiciones explícitas e ímplicitas de este sistema: la aceleración del centro de masa y la aceleración angular deben ser cero ambas; la fuerza de rozamiento estática debe estar dentro del rango de valores posibles; las fuerzas de contacto que ejercen las superficies tienen que apuntar hacia afuera de las superficies (la normal que ejerce el piso no puede ser hacia abajo, la fuerza que hace la esquina no puede ser hacia adentro de la esquina).

----

Para el otro ejercicio, mi sugerencia es plantear el diagrama de fuerzas del cuerpo, dibujado con una pequeña separación con respecto a su posición de equilibrio. Utiliza las ecuaciones de movimiento y de vínculo para calcular la aceleración (y la aceleración angular) en función del desplazamiento respecto al punto de equilibrio. Deberías poder llegar (luego de algunas cuentas) a la ecuación del oscilador armónico simple, con la estructura matemática

$\dfrac {d^2 x} {d t ^2} + \omega^2 x = 0$

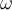donde $\omega$ es una constante que depende de los parámetros del sistema. El período de las oscilaciones es $T=2\pi/\omega$.

Para contestar la pregunta hay que comparar los períodos entre sí para los diferentes casos considerados. Por ejemplo, si observas que $T \propto \sqrt m$, entonces si la masa es mayor pero los demás parámetros se mantienen, el período será mayor; etc.

---

Suerte,
NC