Buenas tardes, estoy intentando resolver este ejercicio pero no logro llegar al valor de velocidad angular correcto, adjunto lo que hice para que puedan decirme donde me estoy equivocando
Espero ser clara y que puedan ayud arme, saludos!
arme, saludos!
Buenas tardes, estoy intentando resolver este ejercicio pero no logro llegar al valor de velocidad angular correcto, adjunto lo que hice para que puedan decirme donde me estoy equivocando
Espero ser clara y que puedan ayud arme, saludos!
arme, saludos!
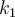 y
y 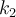 designan constantes que dependen de la constitución material del resorte, y no pueden depender de
designan constantes que dependen de la constitución material del resorte, y no pueden depender de  . La forma en que introduces la posición al final no es correcta.
. La forma en que introduces la posición al final no es correcta.Fijate si puedes tomar en cuenta estás observaciones y plantear una versión revisada del ejercicio y contanos tus avances.
Suerte,
NC
Nicolás muchas gracias por tu respuesta, intenté aplicar lo que me dijiste y si bien llego a un resultado más cercano no es el que debería. Adjunto lo que hice para que puedan corregirme, saludos!

Mucho mejor, pero... la fuerza de rozamiento estática no tiene un valor fijo! En lugar de valer  , su magnitud varía a medida que el cuerpo oscila. Plantea un valor variable
, su magnitud varía a medida que el cuerpo oscila. Plantea un valor variable 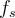 para la fuerza de rozamiento. Recuerda que lo que sabemos solamente es que su módulo cumple la desigualdad
para la fuerza de rozamiento. Recuerda que lo que sabemos solamente es que su módulo cumple la desigualdad  .
.
Hay un par mas de detalles para atender. Convengamos que el dibujo que hiciste, el cilindro acelera en el sentido positivo del eje horizontal, y que su aceleración angular tiene signo positivo. De este modo, como rueda sin deslizar, se cumple  . Pero al hacer esto ímplicitamente estamos estableciendo cual es el sentido positivo para un eje perpendicular al dibujo. En particular, cuando calculamos los torques, debemos respetar este sentido. Por ejemplo, el torque debido a la fuerza de rozamiento queda saliente al dibujo, en sentido contrario a la aceleración angular y, por lo tanto, negativo.
. Pero al hacer esto ímplicitamente estamos estableciendo cual es el sentido positivo para un eje perpendicular al dibujo. En particular, cuando calculamos los torques, debemos respetar este sentido. Por ejemplo, el torque debido a la fuerza de rozamiento queda saliente al dibujo, en sentido contrario a la aceleración angular y, por lo tanto, negativo.
Los estiramientos de los resortes son  y
y  . Como los resortes tienen longitud natural nula, debemos dar algunos pasos adicionales para encontrar el vínculo correcto. Llamemos
. Como los resortes tienen longitud natural nula, debemos dar algunos pasos adicionales para encontrar el vínculo correcto. Llamemos  a la posición de equilibrio del centro del disco, medida desde la pared izquierda, y
a la posición de equilibrio del centro del disco, medida desde la pared izquierda, y 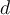 a la distancia entre las paredes. Cuando el centro del disco se mueve una pequeña cantidad
a la distancia entre las paredes. Cuando el centro del disco se mueve una pequeña cantidad 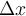 desde la posición de equilibrio, los estiramientos de los resortes quedan
desde la posición de equilibrio, los estiramientos de los resortes quedan  y
y  (como rueda sin deslizar,
(como rueda sin deslizar,  ).
).

Luego de plantear las ecuaciones de movimiento, deberías llegar a un sistema de ecuaciones similar a
Combinando las ecuaciones, se obtiene la ecuación del oscilador armónico simple. Aunque para la solución completa del movimiento hay que determinar el valor de la posición de equilibrio, afortunadamente el período de las oscilaciones no depende de este valor, de manera que si consigues una ecuación de la forma
se puede determinar el período a partir de  (la constante de la ecuación se puede absorber en un cambio de variables, midiendo el desplazamiento dese la posición de equilibrio).
(la constante de la ecuación se puede absorber en un cambio de variables, midiendo el desplazamiento dese la posición de equilibrio).
Saludos,
NC