Foro de Consultas de Evaluaciones Anteriores

Buenas. Estoy viendo que se han encontrado con una dificultad común en sus varios planteos, que surje de los vínculos que aparecen en el sistema del ejercicio. Las ecuaciones dinámicas están mayormente bien, así que enfoquémonos en el aspecto de los vínculos.

La información del enunciado nos permite realizar las siguientes observaciones:

1. El disco sobre la mesa rueda sin deslizar. Sabemos que su punto más bajo tiene (instantáneamente) velocidad nula.
2. Los discos de la polea están unidos. Tienen que tener la misma velocidad angular y la misma aceleración angular.
3. La cuerda horizontal entre el disco de la mesa y el disco de la polea no desliza. Entonces, la velocidad de los puntos del borde de cada uno tiene que tener el mismo módulo. El módulo de la aceleración tangencial (*) de esos puntos debe también ser el mismo.
4. La cuerda vertical que conecta la polea con el bloque no desliza. Entonces el bloque y los puntos del borde del disco grande tienen que tener velocidad de igual módulo. También tienen que tener el mismo módulo de su aceleración tangencial (*).

(*) Los puntos que están en un movimiento circular tienen una componente centrípeta de aceleración, pero en este ejercicio se utiliza.

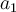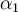A continuación, codifiquemos la información de los vínculos en forma de relaciones entre las variables del sistema. 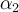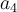Definamos $a_1$ y $\alpha_1$ como los módulos de la aceleración del centro del disco sobre la mesa y de su aceleración angular respectivamente; $\alpha_2$ como el módulo de la aceleración angular del disco de la polea de radio R y $\alpha_3$ como el módulo de la del disco de radio 2R; $a_4$ como la aceleración del bloque.

Usando los vínculos, podemos establecer que:

1. Como el disco de la mesa rueda sin deslizar. Como consecuencia, $a_1 = R \alpha_1$. Otra consecuencia es que el punto (instantáneamente) más alto del disco se mueve el doble de rápido que su centro, con una aceleración $a_c = 2 a_1 = 2 R \alpha_1$.
2. $\alpha_2 = \alpha_3$.
3. Tomando en cuenta el punto más alto del disco sobre la mesa, vemos que el módulo de la aceleración de los puntos de la cuerda tiene que ser 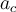$a_c$. Si también tomamos en cuenta el disco de radio R de la polea, vemos que $a_c = R \alpha_2$.
4. Los puntos del borde del disco de radio 2R tienen aceleración tangencial de módulo $a_3 = 2R \alpha_3$, y esta debe ser igual a $a_4$.

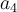Recapitulando y pasando en limpio estas relaciones, nos queda

$a_1 = R \alpha_1$

$2 R \alpha_1 = R \alpha_2$

$\alpha_2 = \alpha_3$

$2R\alpha _3 = a _4$

A partir de lo anterior es posible mostrar, entre otras cosas, que $a_4 = 4 a_1$.

---

La explicación quedó bastante larga, pero quería ser muy explícito en los razonamientos aplicados. Espero que se haya entendido. Fíjense si les ayuda en vuestros planteos y nos cuentan cómo les fue

Saludos,
NC