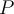Examen Julio 2024 - Ejercicio 8

Examen Julio 2024 - Ejercicio 8

de Guzman Nieves Machado -
Número de respuestas: 3

Buenas, en este ejercicio aplique la conservación del momento angular y despeje la velocidad angular final del sistema, luego intente usar la conservación de la energía para intentar despejar ese ángulo en función de la altura de la partícula con respecto a la horizontal que pasa por el centro pero no pude relacionar la altura de la partícula con respecto al ángulo. No se si es correcto este razonamiento o si hay otro mas fácil.
Gracias


En respuesta a Guzman Nieves Machado

Re: Examen Julio 2024 - Ejercicio 8

de Alexis Sokorov Vargas -
Buenas, yo planteé lo mismo que vos, sólo que al momento de considerar conservación de energía me tomé como inicial \displaystyle E_i = \frac{1}{2} mv_0 ^2 y como final \displaystyle E_f = \frac{1}{2} I^{\text{tot}} \omega ^2 + mgh
donde esa altura la consideré (tomando P como el cero) h=R+d de la siguiente forma:

\alpha = \theta - 90 entonces \displaystyle \sin \alpha = \frac{d}{R} \Rightarrow R\sin\alpha = d \thinspace (R \sin (\theta - 90) = d )
Tuve que fijarme propiedades de seno y coseno y encontré que \sin (90 - \theta) = \cos\theta pero tengo \alpha = \theta - 90 = -(90- \theta) entonces \sin (\theta - 90) = \sin ( -( 90 - \theta) ) = - \sin (90- \theta) = - \cos\theta y, finalmente, llegas a que R\sin(\theta - 90)=-R\cos\theta =d . 
Por lo tanto h=R(1-\cos\theta) y luego sí calculas el ángulo con las energías.

No sé si hay otro método para resolverlo porque si no te acordas de esa propiedad no sé cómo resolverlo
En respuesta a Alexis Sokorov Vargas

Re: Examen Julio 2024 - Ejercicio 8

de Nicolás Casaballe -

Gracias, Alexis! Tu respuesta es correcta. Quería comentar que una de las diferencias con el planteo de Guzmán es el nivel de referencia de la altura: en tu caso el cero está en el punto más bajo del disco, y en el otro está en el centro del disco. Ambas opciones son válidas, y el resultado del ejercicio no depende de esta elección.

Una forma de llegar a la misma relación trigonométrica que obtuviste es considerar un esquema para un ángulo \theta < 90°. Queda algo de este estilo:


donde pienso que queda más evidente la relación que obtuviste. Lo malo es que como en el ejercicio se usa un ángulo \theta = 120° > 90° , es improbable que se nos ocurra hacer un diagrama como este como primera opción.

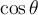El siguiente esquema podría servir para visualizar las relaciones trigonométricas que utilizaste, aunque hay que tomar en cuenta que si 90° < \theta < 270° , entonces \cos \theta es negativo.


En el diagrama podemos comprobar que

R \sin \alpha = R |\cos \theta| = - R \cos \theta

(\alpha = \theta - 90°). No está indicado el ángulo \alpha - 90° para que no quede tan cargado el dibujo, pero supongo que lo pueden identificar fácilmenten.

Saludos,
NC