EJ 10, 2do parcial 1er semestre 2022

EJ 10, 2do parcial 1er semestre 2022

de Julieta Recoba Argul -
Número de respuestas: 2

Buenas tardes, 

dd

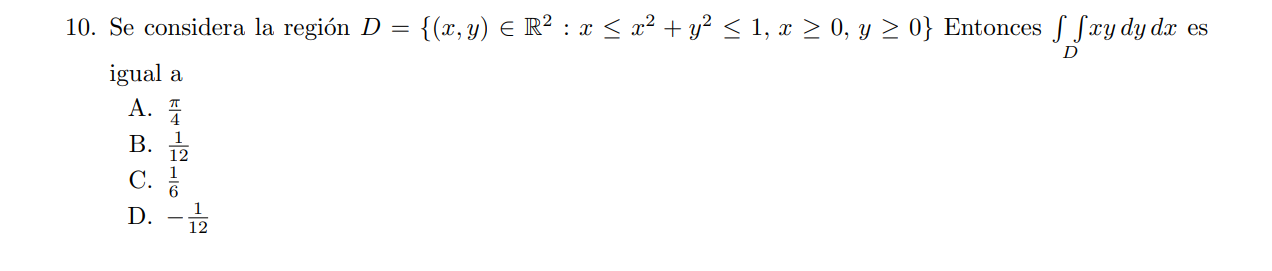
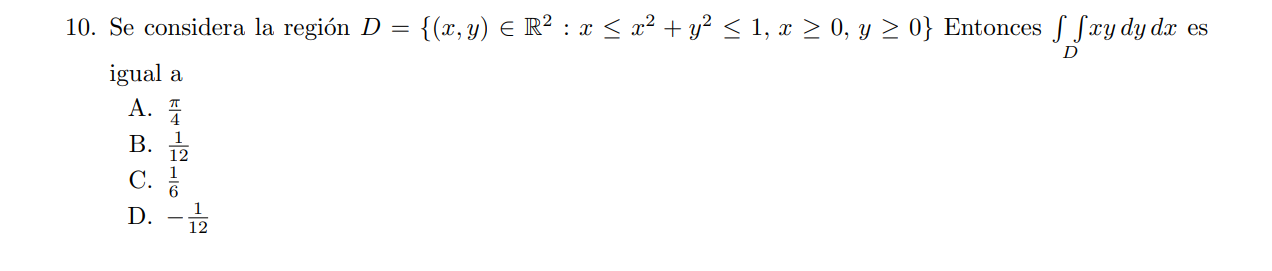
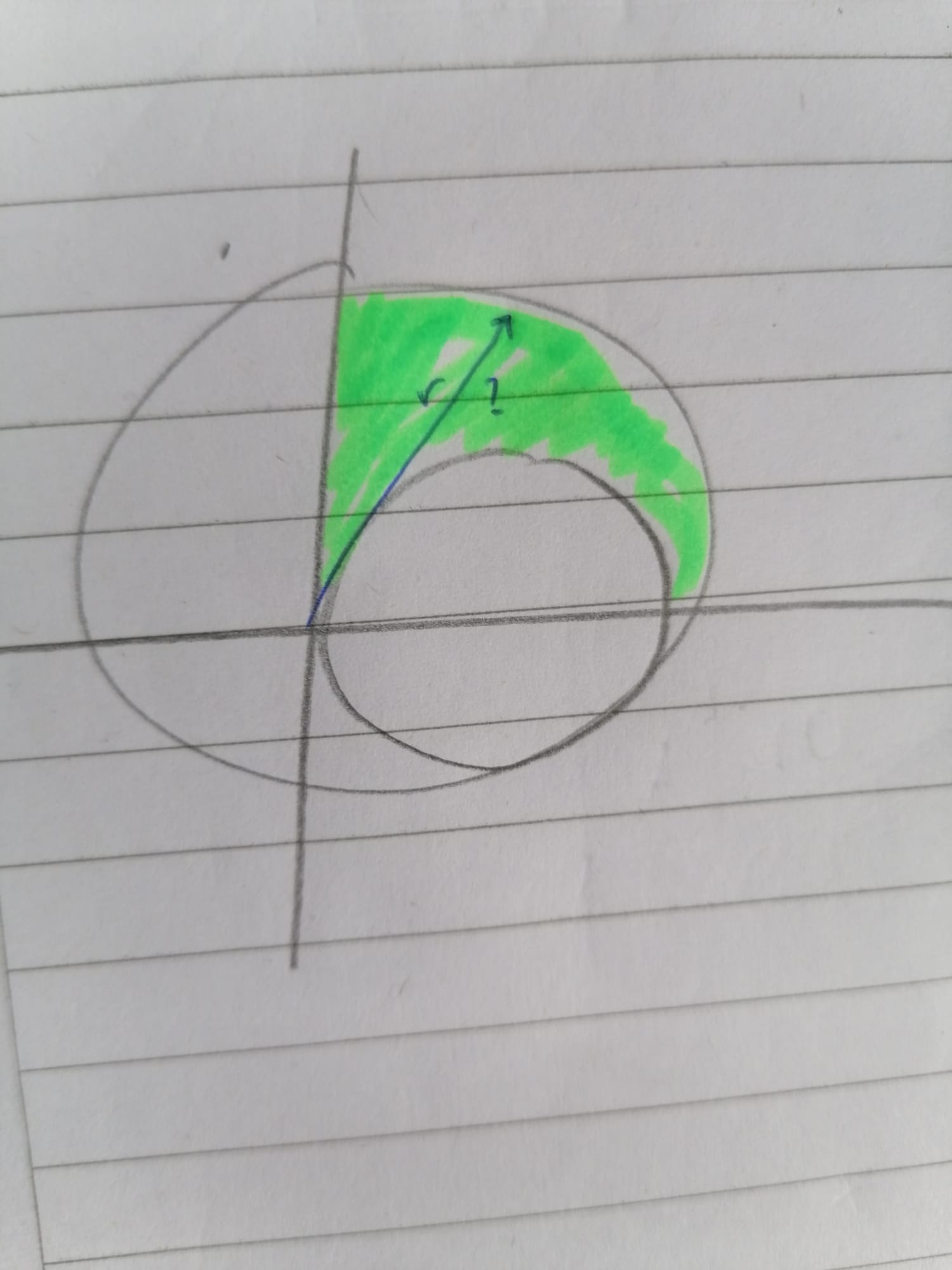
Tengo consultas sobre este ejercicio sobre como despejo r del dominio de integracion. Entiendo que tita va de 0 a pi medios pero no se como despejar r.  el dominio de integracion me quedo como en el dibujo.

En respuesta a Julieta Recoba Argul

Re: EJ 10, 2do parcial 1er semestre 2022

de Rafael Parra -
Hola Julieta,

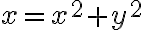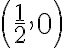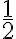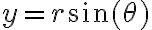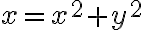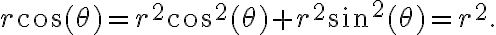
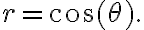
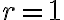La circunferencia x = x^2 + y^2 está centrada en \left(\frac{1}{2}, 0\right) y tiene radio \frac{1}{2}. Para encontrar su ecuación en coordenadas polares, sustituimos x = r\cos(\theta) y y = r\sin(\theta) en la ecuación x = x^2 + y^2:
  r\cos(\theta) = r^2\cos^2(\theta) + r^2\sin^2(\theta) = r^2.
De esta relación, obtenemos que:
r = \cos(\theta).
 Esta es la ecuación de la circunferencia en coordenadas polares, que corresponde al límite inferior de integración. Por otro lado, el límite superior de integración es r = 1.