Buenas,
Estaba realizando el ejercicio 5 del práctico 8:

y noté que no es cierta la afirmación con un contraejemplo:
Las únicas matrices de permutación de 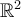 son la identidad y la misma
son la identidad y la misma 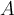 , las cuales son simétricas, por lo que
, las cuales son simétricas, por lo que  matriz de permutación, por lo que
matriz de permutación, por lo que 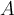 es irreducible.
es irreducible.
Pero  , por lo que existe un entero positivo
, por lo que existe un entero positivo 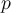 tal que
tal que  es reducible.
es reducible.
Lo que parece que fuera válido es que si 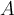 es reducible
es reducible 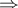
 es reducible, con
es reducible, con 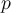 entero positivo.
entero positivo.
¿Será que justo elegí un caso muy puntual?
Saludos.
