Buenas, queria pedir una ayuda con como encarar este ejercicio. Se que es por el lado de oscilacion de un pendulo fisico y que tengo que utilizar la inercia pero estoy trancada. Gracias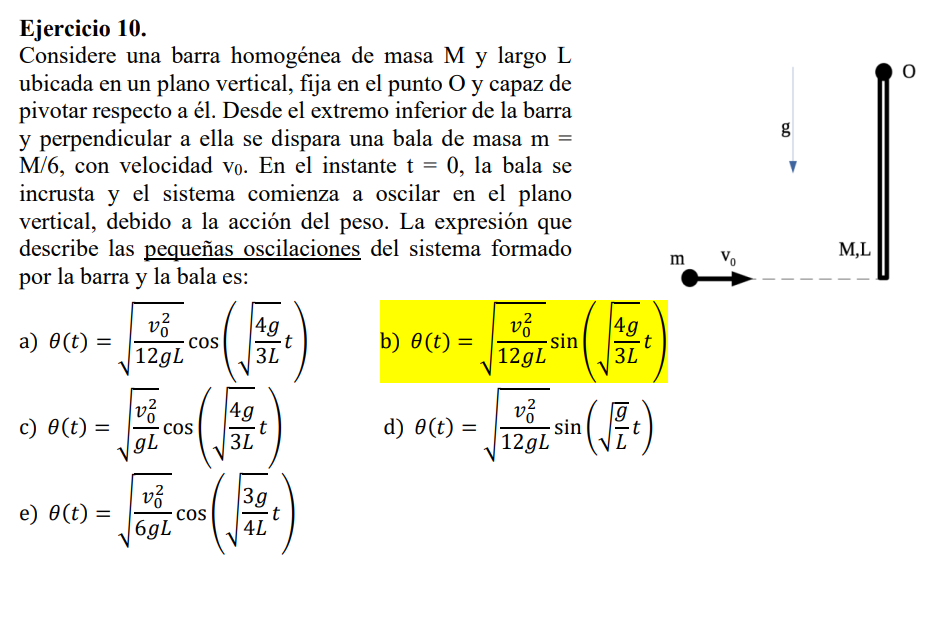
En respuesta a Carolina María Rodríguez Rodríguez
Re: 2do parcial 1s 2022 ej 10
de Alejandro Agesta -
Hola Carolina te dejo una guía con un par de pasos a ver si te ayudan a como encarar el problema:
Paso 1: Armar la ecuación del movimiento
La ecuación general del movimiento tiene la forma:
 (1)
(1)Para pequeñas oscilaciones, se puede aproximar a:
 (2)
(2)cuya solución es:
 (3)
(3)donde
 es el ángulo que forma la barra con la vertical.
es el ángulo que forma la barra con la vertical.Para obtener esta ecuación, analiza dinámicamente el sistema barra+bala (considerando que ambas quedan unidas)
en una posición fuera del equilibrio. Aplicas entonces la segunda cardinal desde un punto seleccionado, por ejemplo si elijes el punto O, entonces se tiene
 (4)
(4)Operando cada término llegarás a la ecuación (1) y de paso determinas 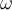
Te dejo un esquema a para que veas un poco mejor la situación
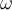
Te dejo un esquema a para que veas un poco mejor la situación
Además de lo anterior para trabajar más cómoda con la segunda cardinal debes elegir un sistema de coordenadas adecuado.
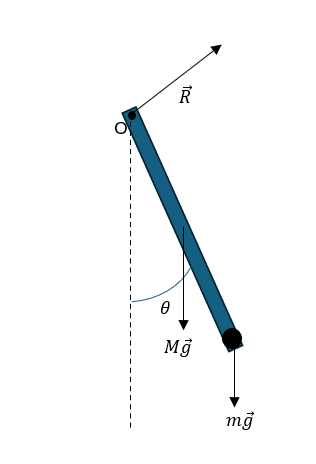
Paso 2: Determinar
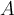 y
y 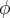 mediante las condiciones iniciales.
mediante las condiciones iniciales.Para determinar
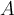 y
y 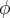 , utiliza las condiciones iniciales evaluando la ecuación (3) y su derivada en t=0t=0:
, utiliza las condiciones iniciales evaluando la ecuación (3) y su derivada en t=0t=0:

Para determinar la velocidad angular inicial del sistema barra+bala utiliza algún principio de conservación (analiza qué cantidad se conserva en este caso durante el choque de la bala).
Adicionalmente te puede ser útil la siguiente relación:

PD: Algunas soluciones se descartan rápidamente según las condiciones iniciales específicas del problema.
Alejandro