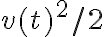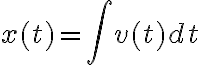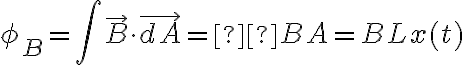Buenas tardes,
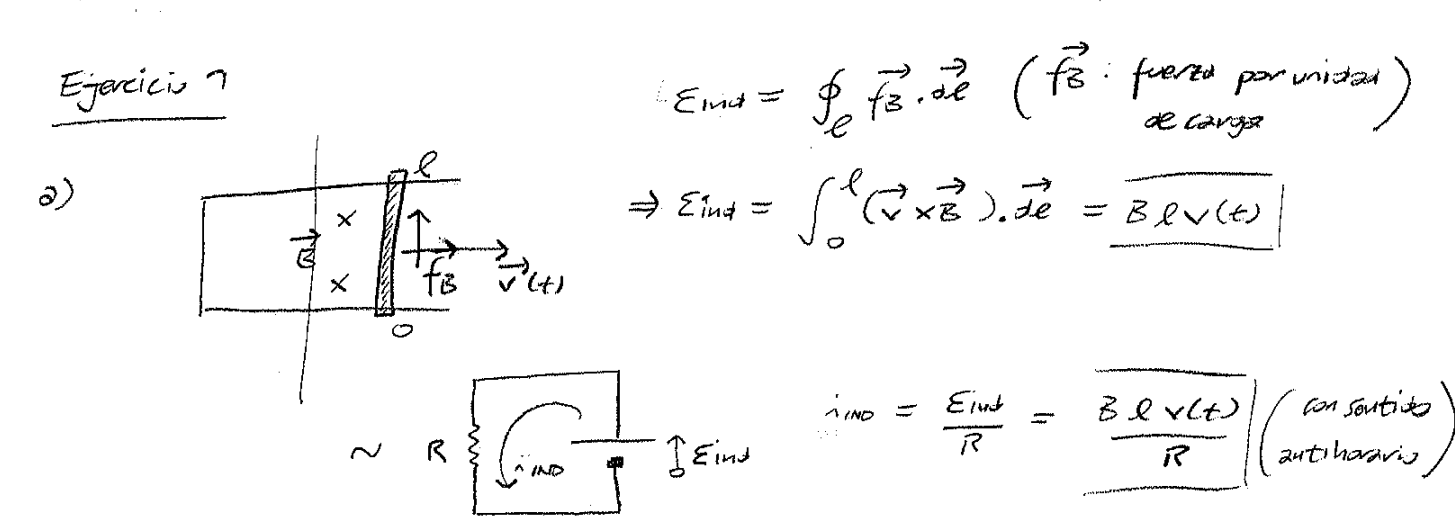
en el ejercicio se pide calcular la fem inducida en el circuito. En las soluciones se resuelve por un camino vectorial. yo seguí otro razonamiento y me gustaría saber si es valido o si estoy perdiéndome de conceptos importantes.
Adjunto ejercicio y la resolución oficial
Gracias