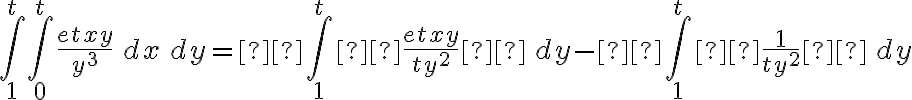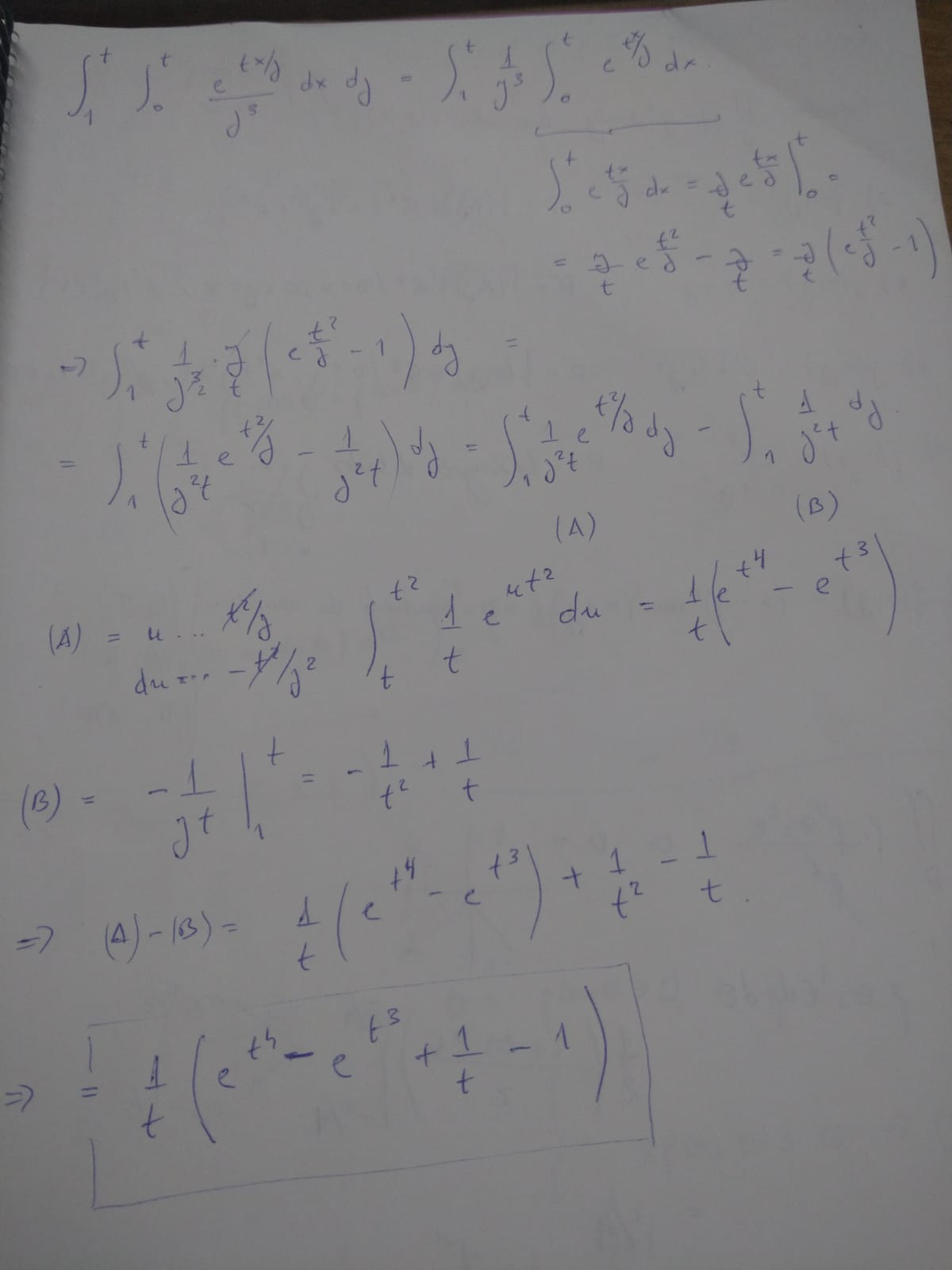Buen día.
En la parte e, no sé cómo queda delimitado el dominio y por ende no sé cuáles son los extremos de integración de la integral doble.
En la parte h, sé resolver la primer integral (de 1 a t, los extremos)dx, pero la integral "de más afuera" de diferencial dy no sé cómo abordarla. Traté con partes sin éxito.
Agradezco una orientación, y si es la resolución mejor aún.
Saludos.
Valentina Andriulis.

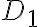
![D_1=[a,b]\times[\alpha(x),\beta(x)] D_1=[a,b]\times[\alpha(x),\beta(x)]](https://eva.fing.edu.uy/filter/tex/pix.php/859d6454c0f09f8776ffaf0f4f633e94.gif)