Buenas, me gustaría saber cómo abordar la parte b de este ejercicio. Lo intenté por varios caminos, pero llega un momento en el que tengo una velocidad que no se cómo hallar. Cómo debería empezar? Gracias
Hola, Luz.
Si interpreto la letra correctamente, hay que separar la situación del ejercicio en dos etapas. Supongamos que en la posición inicial el sistema está en reposo y que, cuando la fuerza F del freno no se aplica, la caja descendió una distancia vertical h. Aunque esto no es explícitamente lo que dice el enunciado, es la única forma en que podemos llegar a una respuesta para la parte (b).
Entonces, calcula la aceleración inicial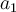 de M (sin la presencia de F) y el desplazamiento
de M (sin la presencia de F) y el desplazamiento 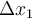 a lo largo del plano si baja una altura h. Hay distintas formas de saber la velocidad del bloque al llegar a esa posición. Pienso que la más corta es utilizar el siguiente resultado para un movimiento con aceleración constante:
a lo largo del plano si baja una altura h. Hay distintas formas de saber la velocidad del bloque al llegar a esa posición. Pienso que la más corta es utilizar el siguiente resultado para un movimiento con aceleración constante:

(utilizando se llega a lo mismo).
se llega a lo mismo).
En la ecuación anterior utiliza y despeja
y despeja 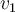 . Esta es la velocidad inicial para la siguiente etapa del movimiento, en la que actúa la fuerza del freno. A continuación el razonamiento es sustancialmente el mismo: hay que hallar la aceleración
. Esta es la velocidad inicial para la siguiente etapa del movimiento, en la que actúa la fuerza del freno. A continuación el razonamiento es sustancialmente el mismo: hay que hallar la aceleración 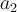 y el desplazamiento
y el desplazamiento 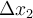 , y nuevamente podemos usar
, y nuevamente podemos usar

Como la caja se detiene en su posición final,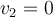 . De ahí se puede despejar
. De ahí se puede despejar 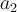 y con esta, presumiblemente, el valor de
y con esta, presumiblemente, el valor de 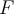 . Me imagino que esta parte ya la tenías planteada.
. Me imagino que esta parte ya la tenías planteada.
Suerte,
NC
Si interpreto la letra correctamente, hay que separar la situación del ejercicio en dos etapas. Supongamos que en la posición inicial el sistema está en reposo y que, cuando la fuerza F del freno no se aplica, la caja descendió una distancia vertical h. Aunque esto no es explícitamente lo que dice el enunciado, es la única forma en que podemos llegar a una respuesta para la parte (b).
Entonces, calcula la aceleración inicial
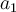 de M (sin la presencia de F) y el desplazamiento
de M (sin la presencia de F) y el desplazamiento 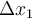 a lo largo del plano si baja una altura h. Hay distintas formas de saber la velocidad del bloque al llegar a esa posición. Pienso que la más corta es utilizar el siguiente resultado para un movimiento con aceleración constante:
a lo largo del plano si baja una altura h. Hay distintas formas de saber la velocidad del bloque al llegar a esa posición. Pienso que la más corta es utilizar el siguiente resultado para un movimiento con aceleración constante:
(utilizando
 se llega a lo mismo).
se llega a lo mismo).En la ecuación anterior utiliza
 y despeja
y despeja 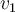 . Esta es la velocidad inicial para la siguiente etapa del movimiento, en la que actúa la fuerza del freno. A continuación el razonamiento es sustancialmente el mismo: hay que hallar la aceleración
. Esta es la velocidad inicial para la siguiente etapa del movimiento, en la que actúa la fuerza del freno. A continuación el razonamiento es sustancialmente el mismo: hay que hallar la aceleración 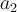 y el desplazamiento
y el desplazamiento 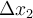 , y nuevamente podemos usar
, y nuevamente podemos usar
Como la caja se detiene en su posición final,
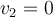 . De ahí se puede despejar
. De ahí se puede despejar 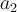 y con esta, presumiblemente, el valor de
y con esta, presumiblemente, el valor de 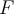 . Me imagino que esta parte ya la tenías planteada.
. Me imagino que esta parte ya la tenías planteada.Suerte,
NC
Muchas gracias profe, no me había dado cuenta de que tenía que suponer que el sistema está en reposo al inicio :)