Estudiantes,
En el practico del lunes de mañana estuvimos trabajando con este ejercicio, que les quedó para resolver (probar que no existe o que existe solución). Les mando la siguiente pista para redondear el problema.
El ejercicio pregunta cuál es la mayor cantidad de vértices que puede tener un grafo con 17 aristas en el que todos sus vértices tengan grado mayor o igual a 3. Usando la fórmula de la suma de los grados es fácil concluir que el máximo de vértices es 11: 10 de ellos de grado 3 y uno de grado 4. Luego pregunta si un tal grafo existe, para los cual les propongo en el dibujo adjunto observar que existe un grafo con 4 vértices de grado 3 y uno de grado 4, el cual se obtiene a partir de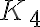 
--único grafo 3-regular de 4 vértices--, agregando uno en el centro, en el cruce de las dos diagonales. Les propongo entonces ver si es posible generalizar este principio para encontrar una solución de 11 vértices al problema.
Más en general, aprovechando el ejercicio para hacerse otras preguntas, cabe preguntarse si existen soluciones con menos vértices (aumentando el grado de ellos, claro). Por ejemplo, si existe un grafo con 6 vértices de grado 5 y uno de grado 4; ya que esa configuración no entra en contradicción con la fórmula de suma de los grados. ¿Cuántas configuraciones posibles son consistentes con la fórmula de suma de los grados? En alguna configuración para la que hallen al menos una solución, ¿es esta única a menos de isomorfismos?
¡Buen trabajo!
Mauricio Guillermo.