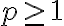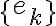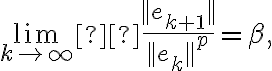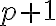Verificar orden de convergencia computacionalmente

Verificar orden de convergencia computacionalmente

de Pedro Gonçalves Schwingel -
Número de respuestas: 3

Hola, estoy un poco perdido en como hacer eso, por ahora lo que estoy haciendo es guardar en un vector los errores que obtengo a cada paso e de alguna forma mostrar que \frac{e^{k+1}}{e^{2k}} \neq 0 esta bien eso ?
En respuesta a Pedro Gonçalves Schwingel

Re: Verificar orden de convergencia computacionalmente

de Lucas Nahuel De Leon Machado -
Hola,

Si método tiene orden p\geq1, entonces la sucesión de errores \{e_k\} cumple

\lim_{k\to\infty} \frac{||e_{k+1}||}{||e_{k}||^p}=\beta,

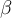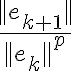para cierto \beta que llamamos la velocidad del método. Entonces, si quieres ver que un método tiene orden p tienes que calcular estos cocientes \frac{||e_{k+1}||}{||e_{k}||^p} y ver si se acercan a algún valor positivo (Si parecen irse a 0 posiblemente el orden es mas grande).

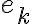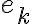Supongamos que errores es el vector en Octave que guarda los e_k, entonces norm(errores(2:end))./norm(errores(1:end-1))^p es una forma rápida de calcular los cocientes de arriba.

Saludos.
En respuesta a Lucas Nahuel De Leon Machado

Re: Verificar orden de convergencia computacionalmente

de Pedro Gonçalves Schwingel -
Gracias por la respuesta, todavía hay algo que no entiendo: hice un programa que itera sobre p y chequea si con el p+1 obtuvo un valor menor para el cociente descrito arriba, el tema es que con eso llego a un orden mucho mas grande de lo que piden chequear, se cumple que si es orden p+1 entonces es orden p? quieren que hagamos la iteracion o que simplemente constatemos que el límite existe y es positivo?
En respuesta a Pedro Gonçalves Schwingel

Re: Verificar orden de convergencia computacionalmente

de Lucas Nahuel De Leon Machado -
Si haces los cocientes subestimando el orden, deberías obtener que los cocientes se van a cero (osea si el metodo tiene orden p+1, entonces los cocientes poniendo p deberían irse a cero).

Para ver el orden hay que ver que el limite existe y es positivo.