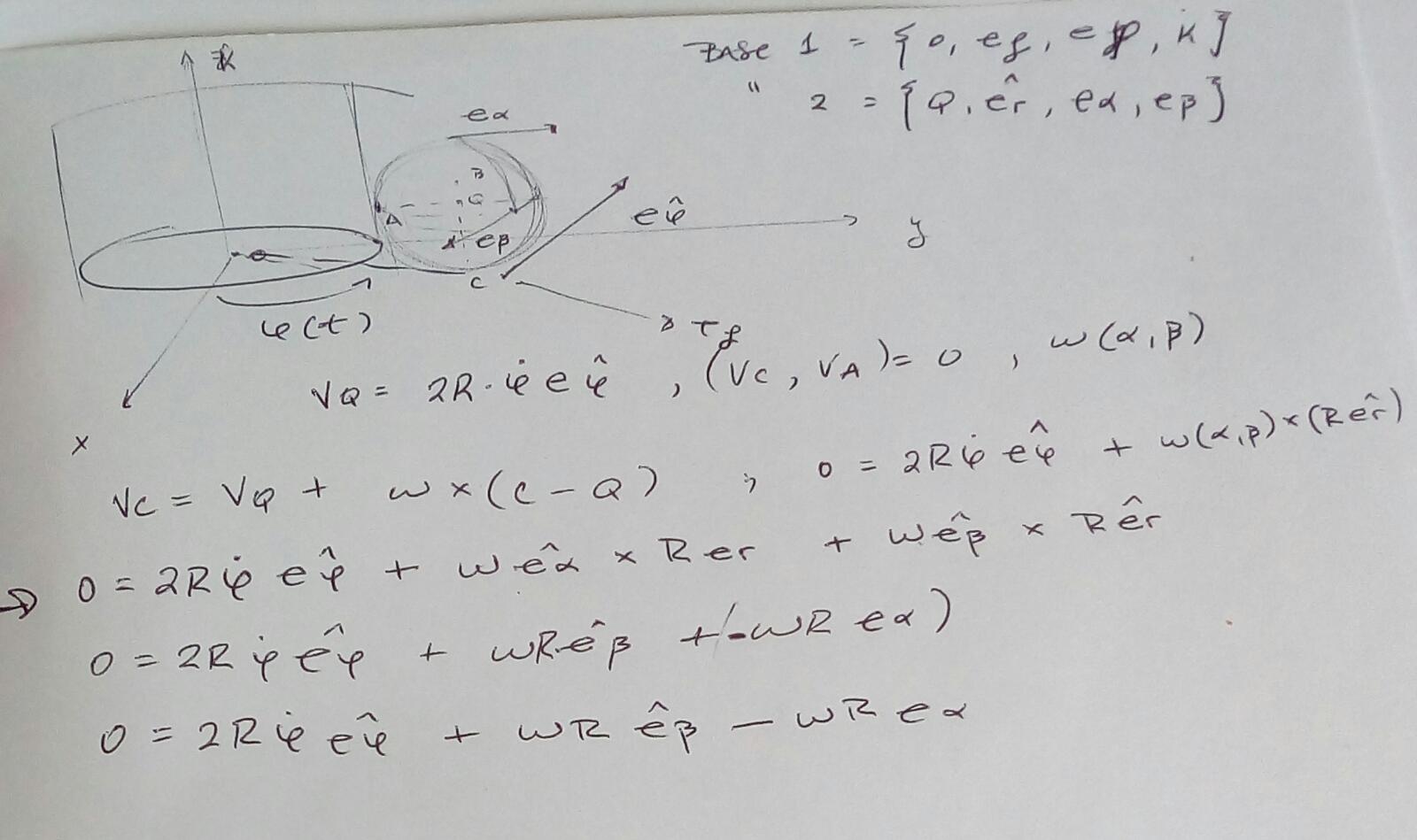
Hola, me surgieron algunas dudas con este problema. Primero defini una base de versores de cilindricas centrados en O eφ, eρ, k y tambien unos versores de esfericas centrados en Q, eα (que mide el angulo polar) eβ (que mide el angulo azimutal). Luego observe que el punto Q recorre una trayectoria conocida y calcule su velocidad como VQ=2R(φpunto) eφ, y ademas que la velocidad de A y C por ser puntos de contacto es inst nula. Llegue a la distribucion de velocidades del rigido y escribi la velocidad angular genericamente en terminos de α y β comparando las velocidades de A y C con Q, el problema es que ambas ecuaciones me darian la misma informacion y que luego la velocidad de Q me queda segun eφ y el producto vectorial me queda segun eα o eβ al descomponer la velocidad angular en sus coordenadas y no se como descomponerlos para que me quede segun eφ
Hola Ivan, disculpa la demora en la respuesta.
Para resolverlo como lo estás pensando vos tendrías que definir los vectores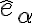
y 
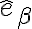en términos de la base de cilíndricas. Hay una manera más sencilla y es la siguiente: como vos mencionaste 
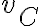y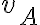 
son ambos cero, por lo que si hago distribución de velocidades entre ellos dos llego a 
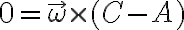. Esta ecuación me dice que la vel angular es colineal a (C-A), y puedo trabajar siempre en la base de cilíndrias. Para determinar el módulo ahora uso distribución de velocidades pero con otro punto.
Pensalo y cualquier cosa consultanos.
Saludos!
Para resolverlo como lo estás pensando vos tendrías que definir los vectores
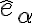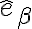y en términos de la base de cilíndricas. Hay una manera más sencilla y es la siguiente: como vos mencionaste 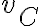y 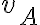son ambos cero, por lo que si hago distribución de velocidades entre ellos dos llego a 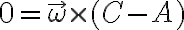. Esta ecuación me dice que la vel angular es colineal a (C-A), y puedo trabajar siempre en la base de cilíndrias. Para determinar el módulo ahora uso distribución de velocidades pero con otro punto. Pensalo y cualquier cosa consultanos.
Saludos!