Buen día, no logro entender la diferencia entre estas dos. y por tanto por que si el reciproco del b) es falso, por que se sigue cumpliendo el a). Muchas gracias.
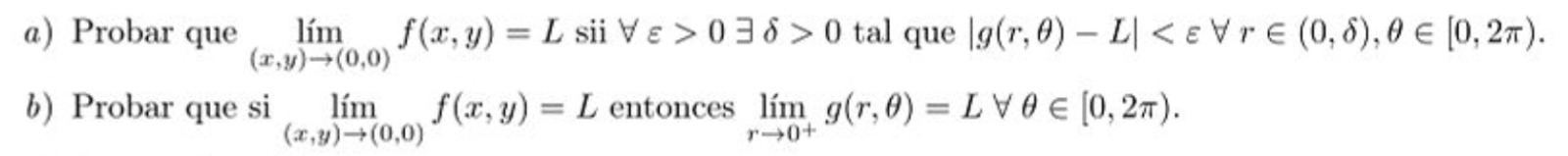
Buen día, no logro entender la diferencia entre estas dos. y por tanto por que si el reciproco del b) es falso, por que se sigue cumpliendo el a). Muchas gracias.
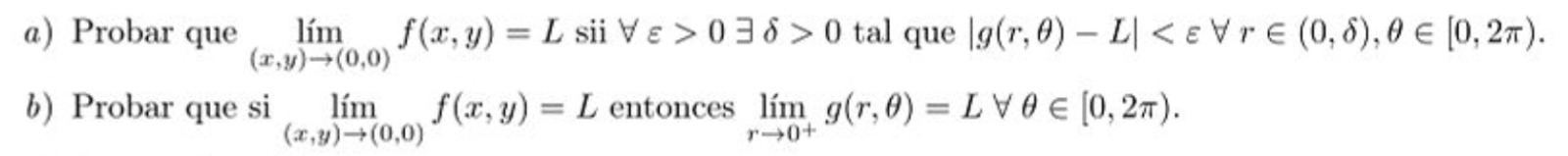
Hola, Tomás, en el a) es una equivalencia con la definición de límite, ya que lo que está después del sii es la definición de límite utilizando coordenadas polares solamente: si el módulo r es pequeño y cualquier ángulo (osea el punto está cerca del origen), entonces f(punto cerca del origen) va a estar cerca de L.
La b) sin embargo dice que si el límite existe y es L, entonces existen todos los límites direccionales (es decir, fijando theta y haciendo tender r a cero). Pero como vimos en clase, el recíproco no se cumple, es decir, pueden existir todos los límites direccionales y sin embargo no existir el límite.
La diferencia entre a) y b) es que en a) es la definición de límite, tomando en cuenta todos los puntos cercanos al origen y en b) solo se restringe la función a semirrectas, esto es, fijando un theta en [0,2\pi) y haciendo rho tender a cero. Osea, sólo te acercás al origen por la semirrecta que sale del origen con ángulo theta en sentido antihorario medido desde el semieje Ox. Fijate que en el lado derecho de b) theta está fijo, y solo se mueve rho.