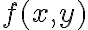Foro Práctico 7

Hola, mi punto débil son las demostraciones matemáticas y por lo tanto me gustaría mejorarlas. Me parece que este es un buen ejercicio para empezar. 

Entiendo que me está pidiendo probar que un límite cuando (x,y) tiende a (0,0) de f(x,y) converge a un L dado si y solo si se dan las condiciones dadas en amarillo. 

Esa condición, es que 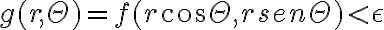$g(r, \Theta)=f(r cos \Theta,r sen \Theta) < \epsilon$ (Corregirme si esto está mal)
Además, como es un sii, se cumple para ambos lados de la ecuación. Por lo tanto habría que probarlo 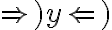$\Rightarrow) y \Leftarrow)$
El problema es que no sé como comenzar. ¿Qué escribir? ¿Cómo demostrarlo? 

Quedo pendiente de una respuesta, un saludo y gracias.