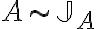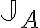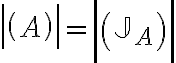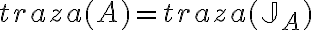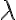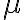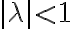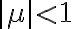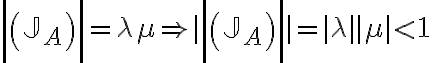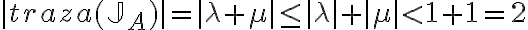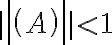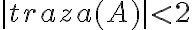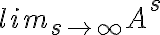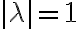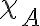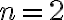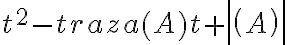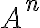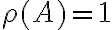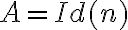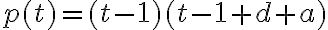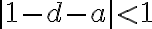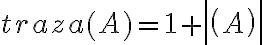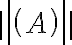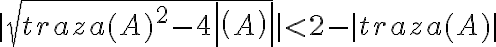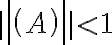AALI-2S: Ejercicio 4 del práctico 4

Buenas tardes. Junto con Agus tenemos una duda sobre el ejercicio mencionado. Logramos hacer la caracterización cuando el radio espectral es 1, pero no encontramos condiciones sencillas para el caso radio espectral menor a 1 y vaps distintos.

Si alguien tiene algún pique, nos vendría bárbaro.

Saludos

Agus y Gonza

Re: Ejercicio 4 del práctico 4

de Vicente Julio Fourment Durán - sábado, 28 de septiembre de 2024, 17:53

Hola,

Yo lo pensé usando el determinante y la traza para los valores menores que uno y vaps distintos.

Recordando que $A \sim \mathbb{J}_A$ , con $\mathbb{J}_A$ la matriz de Jordan asociada a $A$ entonces $det(A) = det(\mathbb{J}_A)$ y $traza(A) = traza(\mathbb{J}_A)$ .

Sean $\lambda$ y $\mu$ los vaps de $A$ , y les exigimos que $\mid\lambda\mid < 1$ y $\mid\mu\mid < 1$ .

Entonces, calculando la norma del determinante de $\mathbb{J}_A$ , $det( \mathbb{J}_A) = \lambda \mu \Rightarrow \mid det( \mathbb{J}_A) \mid = \mid\lambda\mid\mid\mu\mid < 1$

Y calculando la norma de su traza y usando esigualdad triangular: $\mid traza(\mathbb{J}_A) \mid = \mid \lambda + \mu \mid \leq \mid \lambda \mid + \mid \mu \mid < 1 + 1 = 2$ .

Como la traza y el determinante son funciones invariantes bajo semejanza, si se cumple que $\mid det(A) \mid < 1$ y $\mid traza(A) \mid < 2$ entonces $lim _{s \rightarrow \infty }A^s$ converge.

Me interesaría saber qué condiciones tiene que tener A cuando el radio espectral es 1 concluyeron, si no es molestia.

Re: Ejercicio 4 del práctico 4

de Vicente Julio Fourment Durán - sábado, 28 de septiembre de 2024, 19:11

Acabo de darme cuenta que para el caso que

$\mid \lambda \mid = 1$ , también se cumplen estas condiciones. Por lo que no se cumple exclusivamente para loa que tengan norma menor que 1.

Re: Ejercicio 4 del práctico 4

de Vicente Julio Fourment Durán - sábado, 28 de septiembre de 2024, 19:36

La mejor condicion a la que pude llegar a fue a partir de hallar explícitamente las raíces de

$\chi_A$ , una recomendación es trabajar con que el polinomio característico, en el caso de

$n=2$ es

$t^2 - traza(A)t + det(A)$

Re: Ejercicio 4 del práctico 4

de Agustin Ignacio Estramil Dimello - sábado, 28 de septiembre de 2024, 20:39

Hola,
Muchas gracias! Nosotros habíamos considerado la forma genérica de una matriz de 2x2,

$A= \begin{pmatrix}a & b\\c & d\end{pmatrix}$

Para que el límite de

$A^n$ exista, en el caso

$\rho(A) = 1$ tiene que cumplirse además que 1 sea el único valor propio de módulo 1 y además que MG(1)=MA(1).
Si MG(1)=2 entonces

$A = Id(n)$ . Si MG(1)=MA(1)=1 entonces el polinomio característico puede factorizarse como

$p(t) = (t-1)(t-1+d+a)$ de donde concluimos que

$|1-d-a| < 1$ .
Saludos.

Re: Ejercicio 4 del práctico 4

de Vicente Julio Fourment Durán - sábado, 28 de septiembre de 2024, 22:19

Algo que noto es que en el MA(1) = 1, no están imponiendo condiciones para c y b, lo cual, en mi opinión son importantes para que 1 sea raíz de

$\chi_A$ .

La condición a la que llegué yo fue:

$traza(A)=1+det(A)$ , con

$\mid det(A) \mid$ , esto lo obtuve al reemplazar 1 en

$\chi_A$ , y luego la condición del determinante la saqué directamente de que

$\mid det(a)\mid = \mid\lambda\mu\mid = \mid\mu\mid < 1$

Re: Ejercicio 4 del práctico 4

de Oscar Santiago Vallejo Sanchez - sábado, 28 de septiembre de 2024, 20:33

La matriz siguiente cumple que el valor absoluto de su traza es menor a 2, que el valor absoluto de su determinante es menor a 1 e igual no converge la sucesion A^s
A= 1,5 0
0 0,3

En un principio había llegado a las mismas conclusiones que vos Vicente, pero no son CNyS.

Si llegas a encontrarle la vuelta por favor comparte!

Gracias.

Re: Ejercicio 4 del práctico 4

de Vicente Julio Fourment Durán - sábado, 28 de septiembre de 2024, 22:03

Llegué a la misma condición que un compañero:

Para valores propios con norma menor que 1, se tiene que cumplir que:

$\mid \sqrt{traza(A)^2 - 4det(A)} \mid < 2 - \mid traza(A) \mid$

Esto sale directamente de la fórmula de Bhaskara y sabiendo que la norma de los valores propios son menores que 1.

Los demás casos admiten condiciones más "fáciles,¨ como muestran Gonzalo y Agus más arriba.

Por ejemplo, una condición que encontré para el caso que tenga un solo valor propio 1, es que

$traza(A) = 1 + det(A)$ , con

$\mid det(A) \mid < 1$