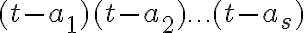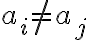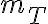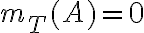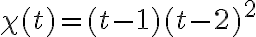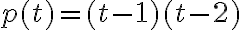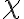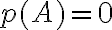Práctico 3 ejercicio 2

Práctico 3 ejercicio 2

de Agustin Ignacio Estramil Dimello -
Número de respuestas: 8

Buenas noches!

Estamos con Gonza haciendo este ejercicio y nos surge la siguiente duda: 

Estamos intentando probar que a implica b, pero hay algo que no nos cierra.

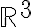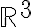Si consideramos la transformación lineal de \mathbb{R}^3 en \mathbb{R}^3 con matriz asociada 

 A = \begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\0 & 0 & 1 \end{pmatrix}
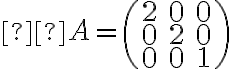
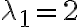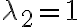Sabemos que esa matriz tiene valores propios \lambda_1 = 2 y \lambda_2 = 1 y polinomio minimal 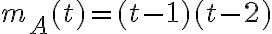m_A(t) = (t-1)(t-2) o sea que de acuerdo al ejercicio 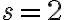s=2 , por lo que si el enunciado a implica el b tendríamos una base de 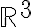\mathbb{R}^3 con dos vectores. 
No entendemos en qué nos estamos equivocando.
Gracias de antemano.
Saludos,
Gonza y Agus.
En respuesta a Agustin Ignacio Estramil Dimello

Re: Práctico 3 ejercicio 2

de Vicente Julio Fourment Durán -
Hola,

En la letra dice que el polinomio minimal es de la forma (t-a1)(t-a2)...(t-an), con ai≠aj para todo i≠j. Lo que te está diciendo es que la matriz tiene n valores propios distintos.
Justo en ese ejemplo, 2 tiene MG = s = 2, lo que no cumple la hipótesis.

¡Saludos!
En respuesta a Vicente Julio Fourment Durán

Re: Práctico 3 ejercicio 2

de Agustin Ignacio Estramil Dimello -
Gracias Vicente. Pero en la letra del práctico veo que dice algo ligeramente distinto: (t-a_1)(t-a_2)\ldots(t-a_s), con a_i\neq a_j para todo i≠j y no dice que s sea la dimensión de V.
En respuesta a Agustin Ignacio Estramil Dimello

Re: Práctico 3 ejercicio 2

de Vicente Julio Fourment Durán -
Ah, mis disculpas, era tarde en la noche y pensé que "s" era el exponente de (t-ai).
Pero el punto sigue en pie, el polinomio minimal se descompone en un producto de s monomios con s raíces distintas, el ejemplo que proponen tiene una raíz doble 2.
Saludos.
En respuesta a Vicente Julio Fourment Durán

Re: Práctico 3 ejercicio 2

de Agustin Ignacio Estramil Dimello -
Buen día! Gracias de nuevo pero sigo sin estar de acuerdo ( o sin entender).
Según entiendo el polinomio minimal m_T es un polinomio de menor grado que el característico que divide al característico y que además cumple m_T(A) = 0. El característico de esta matriz es \chi(t) = (t-1)(t-2)^2 que tiene una raíz doble. El polinomio p(t) = (t-1)(t-2) divide a \chi pero además p(A) = 0 entonces p es el minimal y tiene dos raíces simples.
Saludos.
En respuesta a Agustin Ignacio Estramil Dimello

Re: Práctico 3 ejercicio 2

de Vicente Julio Fourment Durán -
Estoy de acuerdo que el polinomio minimal es (t-1)(t-2)², la cuestión es que, por lo menos en la parte a), te dice que el polinomio minimal tiene s raíces distintas (ai≠aj para todo i≠j y la forma es (t-a1)...(t-as)).
Si vamos a la parte b), la base de V tiene s elementos, por lo que la dimisión del espacio es efectivamente s. Entonces eso significa que el polinomio minimal se descompone con s raíces distintas, siendo s la dimensión de V.
En respuesta a Vicente Julio Fourment Durán

Re: Práctico 3 ejercicio 2

de Angela Natalia Bernardo Baldivieso -
Buen día: Estoy de acuerdo con que el polinomio minimal tiene s raíces distintas, por lo que creo que b)->a es evidente, porque si existe una base de vectores propios de V con s elementos, s es la dimensión de V, y el minimal, si no me equivoco, en este caso coincide con el característico.
a->b no lo veo, porque solo tener el minimal no nos da la dimensión del espacio.
En respuesta a Vicente Julio Fourment Durán

Re: Práctico 3 ejercicio 2

de Marcelo Lanzilotta -
Hola a todos:
El año pasado hemos detectado varios errores del libro. Y lo fuimos limpiando. Este es un error también del libro, que lo habíamos detectado, pero (mal yo!) me olvidé cambiarlo en su momento.
Observen que la redacción del ejercicio coincide con la redacción del Ejercicio 1, página 39, del Capítulo I del libro.
Ya mismo corrijo la letra del Ejercicio.
Incluyo aquí también la corrección:
en la parte b. hay que cambiar s por n. Es decir, debiera decir:

b. Hay una base {v_1,··· ,v_n} de V tal queT(v_j)=a_j.v_j,con j =1,2,...,n, con a_j∈k.