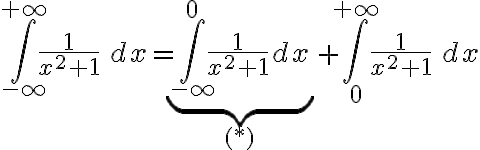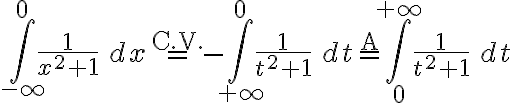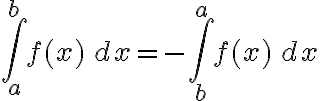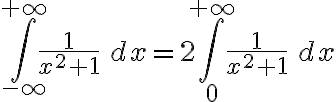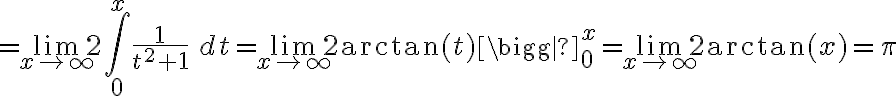Foro Práctico 5

Hola Lucía, gracias por hacer énfasis en esto.

Efectivamente la integral 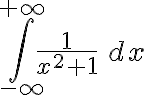$\int_{-\infty}^{+\infty}\frac{1}{x^2+1}\,dx$ es una integral mixta, y debe ser resuelta partiendo en dos, por ejemplo:

$\int_{-\infty}^{+\infty}\frac{1}{x^2+1}\,dx = \underbrace{\int_{-\infty}^{0}\frac{1}{x^2+1}dx}_{(*)}+\int_{0}^{+\infty}\frac{1}{x^2+1}\,dx$

Notando que en 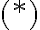$(*)$ se puede aplicar el cambio de variable 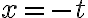$x=-t$, la integral 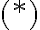$(*)$ resulta:

$\int_{-\infty}^{0}\frac{1}{x^2+1}\,dx \overset{\text{C.V.}}{=} - \int_{+\infty}^{0}\frac{1}{t^2+1}\,dt\overset{\text A}{=}\int_{0}^{+\infty}\frac{1}{t^2+1}\,dt$

Donde en A se utiliza que $\int_a^bf(x)\,dx=-\int_b^af(x)\,dx$.

Es así que la integral impropia del ejericio se re-escribe:

$\int_{-\infty}^{+\infty}\frac{1}{x^2+1}\,dx = 2\int_{0}^{+\infty}\frac{1}{x^2+1}\,dx$

$= \lim_{x\to\infty} 2\int_{0}^{x}\frac{1}{t^2+1}\,dt = \lim_{x\to\infty} 2\arctan(t)\bigg|_0^x = \lim_{x\to\infty} 2\arctan(x) = \pi$

Alguien lo mencionó hoy en una pregunta, pero no hicimos el énfasis necesario.

Retomamos en la clase del miércoles al respecto de esto.

Saludos,

M