Prog3: Práctico 3 - Ejercicio 11

$n$

Buenas, queria compartir mi solucion para saber si la demostracion es correcta, ya que creo que esta un poco floja, el pseudocodigo es

(indeg cuenta la cantidad de aristas entrantes a un nodo)

El algoritmo termina pues los "Para cada" siempre terminan, la unica fuente de bucle infinito posible es el Mientras, aunque en cada iteracion se elimina un elemento del conjunto S,

como ademas solo se agregan vertices y hay tan solo $n$ de ellos, concluimos que itera a lo sumo $n$ veces. Y por tanto todo el algoritmo termina.

Correccion: el algoritmo devuelve un OT si y solo si G tiene un OT

(=>) El algoritmo es analogo al propuesto por el libro (me gustaría saber si esto es una justifiacion suficiente)

(<=) Probaré el contrarreciproco, es decir, el algoritmo no devuelve OT => G no tiene OT

Si el algoritmo no devuelve un OT devuelve un ciclo formado por los nodos v tales que indag[v] != 0, sean estos 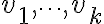$v_1,\dots,v_k$ como cada uno recibe al menos una arista

puedo recorrerlos hacia atras k+1 veces, y debo haber visitado un nodo 2 veces y por tanto halle un ciclo, entonces G no es un DAG y por tanto no admite un OT.

Ahora que demostramos la proposicion anterior, podemos observar que es equivalenta a probar

el algoritmo devuelve un ciclo si y solo si G tiene un ciclo

Pues la negacion de "el algoritmo devuelve un OT" es "el algoritmo devuelve un ciclo", por el If final.

Y la negacion de "G tiene un OT" es, claramente, "G no tiene un OT", que implica que G sea cíclico, pues G es un DAG si y solo si tiene un OT (resultado del libro).

Podemos usar la representacion de lista de adyacencia para el grafo G, recorriendo el conjunto de nodos y aristas, para O(1) por cada elemento podemos crear el grafo en O(m+n)

El primer "Para cada" es O(n), el bucle "Mientras" es O(n) por el mismo argumento que la terminacion y el "Para cada" dentro del "Mientras" se ejecuta a lo sumo m veces sobre todas

las iteraciones del bucle y por tanto podemos concluir que todo el algoritmo es O(m+n)

Re: Práctico 3 - Ejercicio 11

de Facundo Benavides - jueves, 5 de septiembre de 2024, 16:00

hola ezequiel, qué tal?
comento por partes:
a) alg. no es correcto asumir que los nodos v que cuyo indeg(v)!=0 forman un ciclo. p.e. podría pasar que tengas un ciclo en el que algún nodo tiene outdeg=2 y por tanto exista un nodo que no integra el ciclo con indeg=1. todos estos nodos tendrían indeg!=0 pero no forman un ciclo y sería incorrecto devolverlos a todos como integrantes de un ciclo.
lo que sí es cierto, es que en el conjunto de nodos cuyo indeg(v)!=0 existe un ciclo, que el alg debería "descubrirlo" para retornarlo.
b) lo anterior y la prueba de correctitud no pueden ser ambas correctas así que la prueba no es correcta. lo señalo así para que veamos lo importante de realizar pruebas correctas ya que una que no lo sea pude reafirmarnos en el concepto de que nuestro alg es correcto cuando no lo es.
entonces, qué parte de la prueba está mal.
contestando a lo primero que consultás, (=>), la respuesta es que no, no es suficiente (en gral). lo que sí pueden hacer es reutilizar/repetir los mismos argumentos del libro (o los que corresponda) incluyendo propiedades, lemas, teoremas, corolarios, etc sin tener que demostrarlos.
respecto al recíproco (<=), en el primer paso asumís que si no devuelve OT entonces devuelve un ciclo. pero no probás que el conjunto devuelto es un ciclo y allí está el problema. ese enunciado es falso. lo que sigue es correcto pero no implica que el conjunto de vértices defina un ciclo sino algo menos fuerte y es la existencia de un ciclo incluido en ese conjunto.
c) ok
saludos