Hola buenas tardes, tengo una duda de las condiciones que se deben cumplir para encontrar un ciclo.
No me doy cuenta cuando es que puede pasar que llegue a un nodo ya explorado a través de un ciclo, y que se cumple la condición de que llegué a través del padre. Es decir, DFS no nos asegura que si llegamos a un nodo explorado si o si será un ciclo? O porque debería de corroborar que no sea el padre? Muchas gracias
Buenas, yo justo estaba haciendo ese ejercicio y me surgió la misma duda y creo que llegue a un algoritmo bastante encaminado, te lo comparto y te comparto la idea para que comparemos si quieres y si le encontras algún error decime, igual estaría bueno que algún profe lo corrobore también.
Yo hice este algoritmo: (No logre poner como código espero quede bien identado sino pégalo en algún IDE)
Por lo que se ve el algoritmo lo hice recursivo y devuelvo como dos cosas ahí como el booleano si hay ciclo y el ciclo en sí, si es que hay uno.
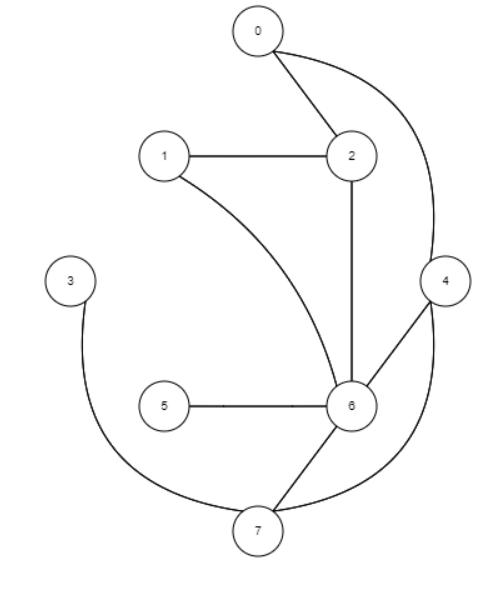
Lo que yo vi es que, me doy cuenta si hay ciclo maso menos por eso que comentas, primero me fijo si el nodo adyacente a la llamada actual (nodo s) ya fue visitado y si ese adyacente (nodo u) esta en el arreglo llamadaPrevia, que quiere decir que no se termino todavía de analizar todas las aristas adyacentes a el mismo, ósea que se sigue dentro de su llamada recursiva por decirlo de alguna manera y si se cumple eso y además (esta es la parte de corroborar que no sea el padre) se cumple que el padre del nodo actual en la llamada, nodo s, no es el nodo adyacente que estoy viendo, ósea u, quiere decir que no estoy viendo la misma arista que me descubrió a mi, entonces vine por otro camino de u a s el cual no incluye la arista (s, u) ahora analizada y junto con ella se forma el ciclo. Es un poco entreverado 😅 pero si lo lees detenidamente creo que se entiende, yo por ejemplo aplique el algoritmo siguiendo el paso a paso para este grafo (el de la imagen) y independientemente de que vayas primero a los nodos mas grandes, del 0 al 4 o del 0 al 2 al mas chico encontras el ciclo correspondiente.
Para la correctitud use la idea que viene del (3.6) Para una llamada recursiva dada DFS(u), todos los nodos que están marcados como visitados entre la invocación de DFS(u) y el final de esta llamada recursiva, son descendientes de u en T.
Si bien acá no construyo árbol la búsqueda en si ya es en forma de árbol DFS y tomando que el nodo esta en llamadaPrevia es un descendiente de u que junto con la arista (s,u) necesariamente formaría un ciclo.
Capaz que iterativo también sale, seguramente con una pila seria igual, pero no lo intente.
Espero algún profe también lo vea y ver si esta bien el algoritmo o al menos la idea general.
Gracias
Yo hice este algoritmo: (No logre poner como código espero quede bien identado sino pégalo en algún IDE)
Function DFS_Cycle(G=(V,E)){
Bool[V] visitados = [False] * |V|;
Nodos[V] padre = [-1] * |V|;
Bool llamadaPrevia[V] = [False] * |V|;
Bool hayCiclo = False;
Cola muestraCiclo = Cola();
For(Int i = 0; i < |V| && !hayCiclo; i++) {
If(!visitados[i]){
(hayCiclo, muestraCiclo) = DFS_Recursivo(G, i, visitados, padre, llamadaPrevia);
}
}
Return (hayCiclo, muestraCiclo);
}
Function DFS_Recursivo(Grafo g, nodo s, Bool[V] visitados, Nodos[V] padre, Bool[V] llamadaPrevia){
visitados[s] = True;
llamadaPrevia[s] = True;
For(nodo u : G.adyacentes(s)){
If(!visitados[u]){
padre[u] = s;
DFS_Recursivo(G, u, visitados, padre, llamadaPrevia);
}Else If(llamadaPrevia[u] && padre[s] != u){
Cola ciclo = Cola();
ciclo.encolar(u);
Nodo actual = s;
While (actual != u){
ciclo.encolar(actual);
actual = padre[actual];
}
ciclo.encolar(u);
Return (True, ciclo);
}
}
llamadaPrevia[v] = False;
Return (False, null);
}
Por lo que se ve el algoritmo lo hice recursivo y devuelvo como dos cosas ahí como el booleano si hay ciclo y el ciclo en sí, si es que hay uno.
Lo que yo vi es que, me doy cuenta si hay ciclo maso menos por eso que comentas, primero me fijo si el nodo adyacente a la llamada actual (nodo s) ya fue visitado y si ese adyacente (nodo u) esta en el arreglo llamadaPrevia, que quiere decir que no se termino todavía de analizar todas las aristas adyacentes a el mismo, ósea que se sigue dentro de su llamada recursiva por decirlo de alguna manera y si se cumple eso y además (esta es la parte de corroborar que no sea el padre) se cumple que el padre del nodo actual en la llamada, nodo s, no es el nodo adyacente que estoy viendo, ósea u, quiere decir que no estoy viendo la misma arista que me descubrió a mi, entonces vine por otro camino de u a s el cual no incluye la arista (s, u) ahora analizada y junto con ella se forma el ciclo. Es un poco entreverado 😅 pero si lo lees detenidamente creo que se entiende, yo por ejemplo aplique el algoritmo siguiendo el paso a paso para este grafo (el de la imagen) y independientemente de que vayas primero a los nodos mas grandes, del 0 al 4 o del 0 al 2 al mas chico encontras el ciclo correspondiente.
Para la correctitud use la idea que viene del (3.6) Para una llamada recursiva dada DFS(u), todos los nodos que están marcados como visitados entre la invocación de DFS(u) y el final de esta llamada recursiva, son descendientes de u en T.
Si bien acá no construyo árbol la búsqueda en si ya es en forma de árbol DFS y tomando que el nodo esta en llamadaPrevia es un descendiente de u que junto con la arista (s,u) necesariamente formaría un ciclo.
Capaz que iterativo también sale, seguramente con una pila seria igual, pero no lo intente.
Espero algún profe también lo vea y ver si esta bien el algoritmo o al menos la idea general.
Gracias
hola ignacio y christian, cómo están?
la situación que consulta ignacio es justamente la que comenta christian.
cuando avanzo sobre v, un hijo de u, veo a u desde v. si no considerara que u es padre de v podría tener la impresión de haber detectado un ciclo que no es tal.
con el arreglo padre alcanzaría para detectar esta situación independientemente de implementar una solución recursiva o iterativa.
saludos
la situación que consulta ignacio es justamente la que comenta christian.
cuando avanzo sobre v, un hijo de u, veo a u desde v. si no considerara que u es padre de v podría tener la impresión de haber detectado un ciclo que no es tal.
con el arreglo padre alcanzaría para detectar esta situación independientemente de implementar una solución recursiva o iterativa.
saludos
