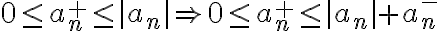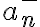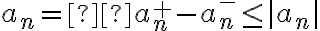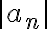CDIVV-2S: Teorema serie A.C. implica C

Tengo una duda sobre si el final de esta demostración del teórico de 2021, clase 14 (dem empieza en 46:10, mi duda es en el min 57:00 aprox), se puede demostrar de otra forma.

Se observa en un momento lo siguiente:

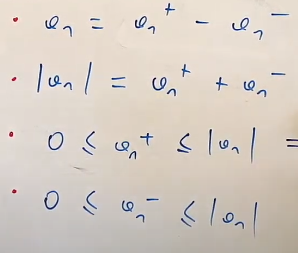
La demostración original finaliza con que la serie de los positivos y negativos convergen, por lo que por el primer punto, an converge también.

Pero utilizando el tercer punto (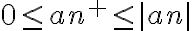 $0 \leq an^+ \leq |an|$ ), si sumo del lado derecho 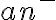$an^-$ que es positivo se mantiene la desigualdad. Restando de ambos lados, quedaría: $an^+-an^- \leq |an|$ .

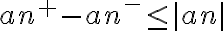Luego, por el primer punto, resultaría en: 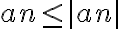$an \leq |an|$

Por hipótesis, |an| es convergente, y entonces por comparación, al ser |an| más grande que an, an tambíen sería convergente.

¿Es esta otra forma de terminar la demostración, o cometo algún error en alguna parte?

Muchas gracias,
Luca.

Re: Teorema serie A.C. implica C

de Mateo Musitelli - martes, 3 de septiembre de 2024, 16:37

Hola Luca, ¿cómo estás?

Es correcto que

$0\leq a_n^{+} \leq |a_n| \Rightarrow 0\leq a_n^{+} \leq |a_n| + a_n^{-}$ , debido a sumar un término positivo, cosa que al restar

$a_n^{-}$ de ambos miembros genera que

$a_n = a_n^{+} - a_n^{-} \leq |a_n|$ .

¿Te das cuenta también que esto tiene sentido debido a que la igualdad de

$a_n$ involucra una resta de términos y la de

$|a_n|$ no?

Quedo atento a tu respuesta,

M

Re: Teorema serie A.C. implica C

de Luca Muiño Irigoyta - martes, 3 de septiembre de 2024, 17:19

Veo que estaría haciendo un paso extra al sumar del lado derecho, ya que la desigualdad seguiría cumpliendose si al lado menor le resto un número positivo. Por lo que llegaría más rápido a la conclusión restando ya en el primer paso.

Muchas gracias por la respuesta, quería saber si por algún motivo no se podía realizar tales operaciones bajo series alternadas, o que no era correcto concluir que por el criterio de comparación, al ser la más grande convergente, también lo sería la más chica. Pero ahora veo que sí cumple esa propiedad, por lo que agradezco nuevamente su rápida respuesta.

Saludos,
Luca.