Hola Lucía, ¿cómo estás?
Es importante considerar en este ejercicio que se solicita que los puntos de aglomeración de la sucesión  a encontrar, deben de ser exáctamente los puntos del conjunto
a encontrar, deben de ser exáctamente los puntos del conjunto 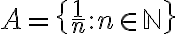 .
.
 a encontrar, deben de ser exáctamente los puntos del conjunto
a encontrar, deben de ser exáctamente los puntos del conjunto 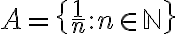 .
.Recordando que punto de aglomeración  de una sucesión
de una sucesión  , es tal que
, es tal que 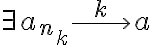 , debemos encontrar una sucesión con una cantidad infinita de subsucesiones convergentes a cada uno de los elementos de
, debemos encontrar una sucesión con una cantidad infinita de subsucesiones convergentes a cada uno de los elementos de  .
.
 de una sucesión
de una sucesión  , es tal que
, es tal que 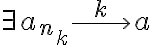 , debemos encontrar una sucesión con una cantidad infinita de subsucesiones convergentes a cada uno de los elementos de
, debemos encontrar una sucesión con una cantidad infinita de subsucesiones convergentes a cada uno de los elementos de  .
.La salvedad aquí es que los puntos de  son un poco particulares, pues son aquellos del recorrido de
son un poco particulares, pues son aquellos del recorrido de 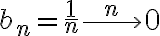 . Esto implica que si existiese una sucesión que cumpla lo que pide el ejercicio, necesariamente el
. Esto implica que si existiese una sucesión que cumpla lo que pide el ejercicio, necesariamente el  deberá pertenecer al conjunto
deberá pertenecer al conjunto  , pero la palabra exáctamente nos lo impide.
, pero la palabra exáctamente nos lo impide.
 son un poco particulares, pues son aquellos del recorrido de
son un poco particulares, pues son aquellos del recorrido de 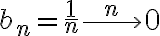 . Esto implica que si existiese una sucesión que cumpla lo que pide el ejercicio, necesariamente el
. Esto implica que si existiese una sucesión que cumpla lo que pide el ejercicio, necesariamente el  deberá pertenecer al conjunto
deberá pertenecer al conjunto  , pero la palabra exáctamente nos lo impide.
, pero la palabra exáctamente nos lo impide.Dejame saber si queda más clara la duda ahora.
Saludos,
M
