CDIVV-2S: Proposición 2.10 (ejercicio de los apuntes)

Hola Mateo:

La hipótesis del ejercicio establece que

$a_n\leq b_n, \forall n in \mathbb N$ .

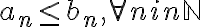Mi comentario va hacie generar lo siguiente:

Para

$a_n$ :

$|a_n-A|< \varepsilon_1, \forall n\geq N_A \Rightarrow A-\varepsilon_1 < a_n < A+\varepsilon_1 , \forall n\geq N_A$ .

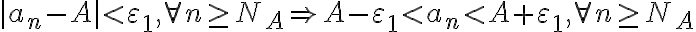Para

$b_n$ :

$|b_n-B|< \varepsilon_2, \forall n\geq N_B \Rightarrow B-\varepsilon_2 < b_n < B+\varepsilon_2 , \forall n\geq N_B$ .

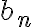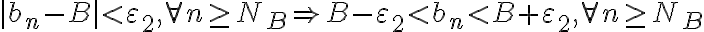Considerando la hipótesis, es posible ver que:

$A-\varepsilon_1 < a_n \leq b_n < B+\varepsilon_2, \forall n \geq N$ .

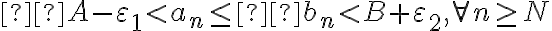Con una correcta elección de

$N$ ,

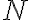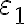$\varepsilon_1$ y

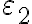$\varepsilon_2$ (te dejo ese análisis), es posible concluir la demostración del ejercicio.

Saludos,

M

Foro de Ejercicios fuera de los Prácticos

Proposición 2.10 (ejercicio de los apuntes)

Re: Proposición 2.10 (ejercicio de los apuntes)