Cuestionario sobre ec diferenciales.

Cuestionario sobre ec diferenciales.

de Mateo Roman Allonca Maldonado -
Número de respuestas: 2

Hola, tengo una duda acerca de un ejercicio del cuestionario. Es el siguiente: 


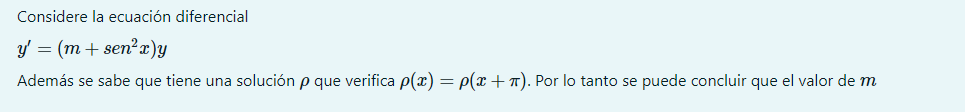
No entiendo que debo hacer con "Además se sabe que tiene una solución p, que verifica p(x) = p(x + pi) ¿Qué información me da? Se que al principio tengo que integrar de ambos lados y'/y = m + sen^2x. Pero, ¿Después que hago cuando tengo la solución? 

En respuesta a Mateo Roman Allonca Maldonado

Re: Cuestionario sobre ec diferenciales.

de Rafael Parra -

Hola Mateo, la solución de esta ecuación diferencial tiene la forma y(x) = C e^{mx +\frac{1}{2} x - \frac{1}{4}\sin(2x)} .

Si verifica la condición    y(x)=y(x+m) , y usando la inyectividad de la función exponencial podemos concluir 

mx +\frac{1}{2} x - \frac{1}{4}\sin(2x) = m(x+\pi) +\frac{1}{2} (x+\pi)- \frac{1}{4}\sin(2(x+\pi))  

De donde m= \frac{-1}{2}