Buenas, ¿Cómo están?
En qué foro se pueden hacer consultas sobre cada cuestionario?
Se pueden hacer o la idea es hacerlas en las clases de práctico?
Gracias
Saludos.-
Buenas, ¿Cómo están?
En qué foro se pueden hacer consultas sobre cada cuestionario?
Se pueden hacer o la idea es hacerlas en las clases de práctico?
Gracias
Saludos.-
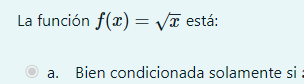


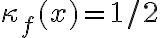 para todo
para todo  . Que el número de condición de
. Que el número de condición de  sea chico no es un problema, sino que al contrario, es algo bueno. Fijate al final de la página 15 de las notas: ahí ves que
sea chico no es un problema, sino que al contrario, es algo bueno. Fijate al final de la página 15 de las notas: ahí ves que 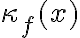 aparece multiplicando en la relación entre el error en la entrada y en la salida al evaluar
aparece multiplicando en la relación entre el error en la entrada y en la salida al evaluar 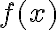 (la fórmula (1.7) muestra eso mismo, pero con un paso más de redondeo y que tiene que ver con la aritmética de punto flotante).
(la fórmula (1.7) muestra eso mismo, pero con un paso más de redondeo y que tiene que ver con la aritmética de punto flotante).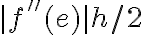 . Para esta función, queda
. Para esta función, queda 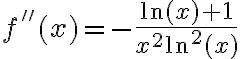 , que al evaluar en
, que al evaluar en  da
da 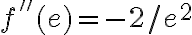 . Con eso, la opción correcta queda
. Con eso, la opción correcta queda 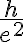 .
.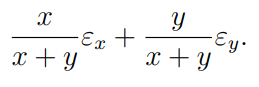
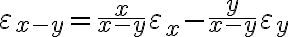 .
.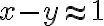 y la desigualdad triangular, queda
y la desigualdad triangular, queda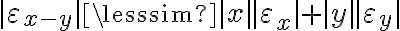 .
.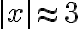 ,
, 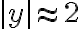 , podés concluir
, podés concluir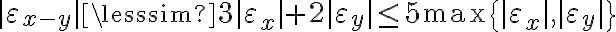 .
. e
e  .
.