Buenas no se me ocurre como hacer este ejercicio
Hola Bryan,
Intentaste algo ya, o no se te ocurre por dónde empezar? Fijate que para hallar las raíces de un polinomio de grado 2 tenés la fórmula de Bhaskara. Usando eso, todo el error viene de aproximar un término que es una raíz cuadrada. Entonces, todo lo que necesitas es saber aproximar raíces cuadradas, que fue discutido en el teórico. Una vez tengas aproximada la raíz, aproximar el error total es sencillo porque simplemente es una resta.
Te sugiero que intentes por este camino, y cualquier cosa preguntes nuevamente.
Saludos!
Intentaste algo ya, o no se te ocurre por dónde empezar? Fijate que para hallar las raíces de un polinomio de grado 2 tenés la fórmula de Bhaskara. Usando eso, todo el error viene de aproximar un término que es una raíz cuadrada. Entonces, todo lo que necesitas es saber aproximar raíces cuadradas, que fue discutido en el teórico. Una vez tengas aproximada la raíz, aproximar el error total es sencillo porque simplemente es una resta.
Te sugiero que intentes por este camino, y cualquier cosa preguntes nuevamente.
Saludos!
Buenas, intente hacerlo como mencionaste y como se explica en el ejemplo 1.3.1 pero necesito primero obtener una de las raíces para obtener la otra, el problema es que en el ejemplo el termino independiente no es chico. Entonces al hacer el discriminante aproximo a raíz de 25? En ese caso me quedaría una de las x=-5 pero esta mal seguramente. Este es el método correcto para realizar el ejercicio? Muchas gracias!
Hola Juan,
Perdón la demora, no quedé suscrito a la discusión y se me pasó contestar.
La idea de este no es usar una aproximación como la de ese ejemplo, sino aprovechar las herramientas que tenés para aproximar funciones. Más explícitamente, podrías intentar usar el número de condición de la función raíz cuadrada para aproximar la raíz cerca de 25 (fijate que lo que le restás al 5 es muy pequeño).
Entonces tomamos la función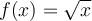
y a partir de eso calculamos el número de condición. Con ese número (que depende de 
), podemos hallar una cota para el error total, que sería la diferencia entre el resultado de la raíz sin aproximar y la raíz de 25. Si el error es chico (menor que 
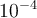por ejemplo), ¿qué te dice sobre la cantidad de dígitos de precisión?
Perdón la demora, no quedé suscrito a la discusión y se me pasó contestar.
La idea de este no es usar una aproximación como la de ese ejemplo, sino aprovechar las herramientas que tenés para aproximar funciones. Más explícitamente, podrías intentar usar el número de condición de la función raíz cuadrada para aproximar la raíz cerca de 25 (fijate que lo que le restás al 5 es muy pequeño).
Entonces tomamos la función
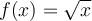y a partir de eso calculamos el número de condición. Con ese número (que depende de ), podemos hallar una cota para el error total, que sería la diferencia entre el resultado de la raíz sin aproximar y la raíz de 25. Si el error es chico (menor que 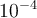por ejemplo), ¿qué te dice sobre la cantidad de dígitos de precisión?