ElecMag: Ejercicio 4) parte a)

Buenas noches, quería consultar por el ejercicio 4) parte a).

Entiendo la sugerencia que se me hace para resolverlo y encuentro que una propiedad útil es 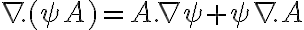$\nabla . (\psi A) = A. \nabla \psi + \psi \nabla . A$ . El ejercicio plantea que 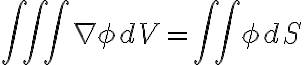$\iiint \nabla \phi dV=\iint \phi dS$ . En principio planteo 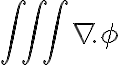$\iiint \nabla . \phi$ en vez de 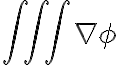$\iiint \nabla \phi$ , ya que sino no puedo usar la propiedad mencionada más arriba y no veo otra que me lleve a buen puerto. Una vez desarrollo el término 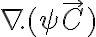$\nabla . 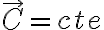(\psi \vec{C})$ con $\vec{C}=cte$ llego a que 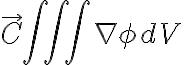$\vec{C} \iiint \nabla \phi dV$ . Luego de esto quisiera aplicar Gauss para buscar la igualdad deseada pero una vez más me encuentro con 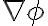$\nabla \phi$ en vez de 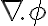$\nabla . \phi$ , lo que me impide usar el teorema de la divergencia.
Les pido ayuda para ver como puedo continuar o si es que alguna de las expresiones no las estoy entendiendo bien.