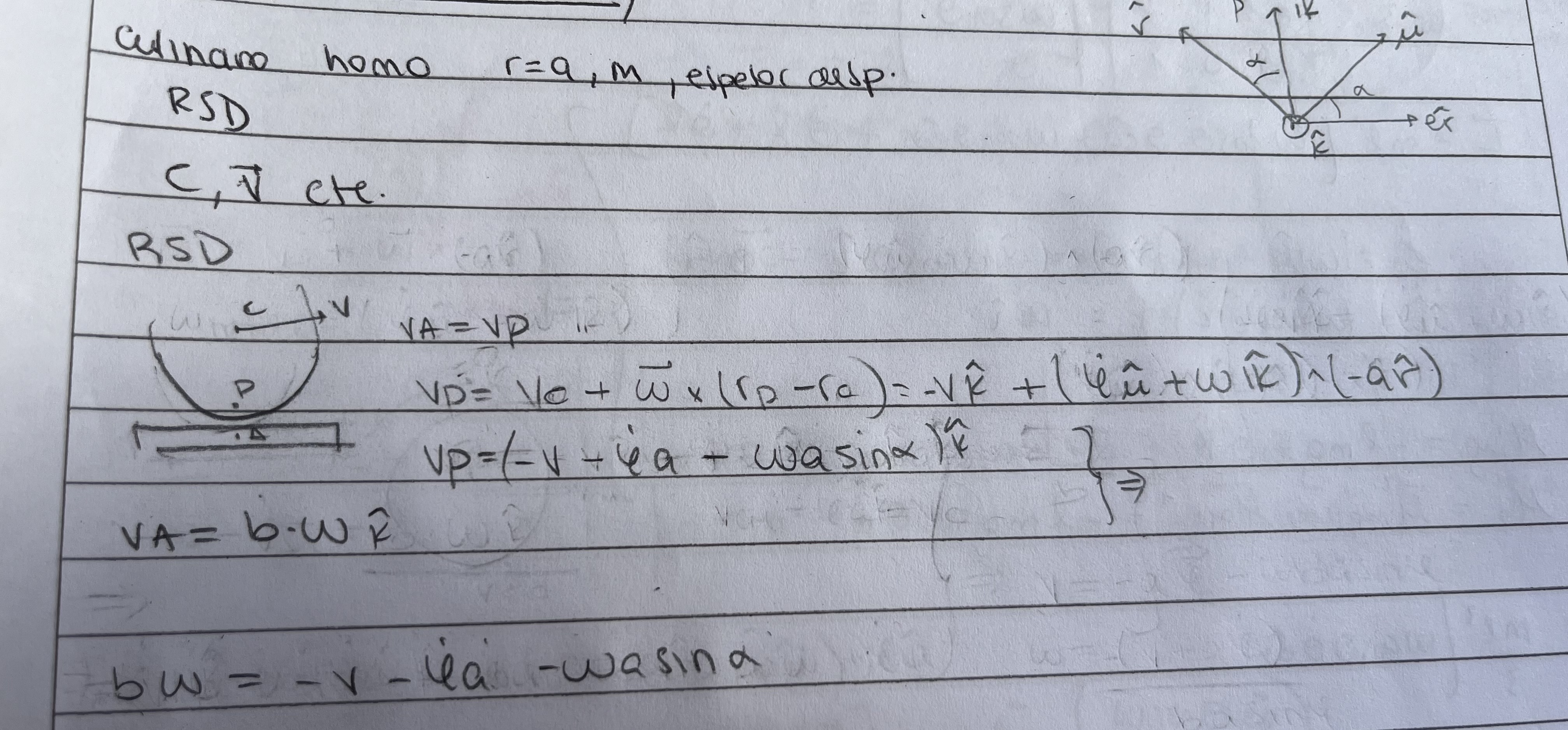Buenas, tenía una duda de por qué en la solución plantearon la condición de rodadura sin deslizar con el movimiento que hace la moneda con respecto al eje K y no con la rotación de la moneda con el eje u, es decir que v= (dΨ/dt) x a
gracias
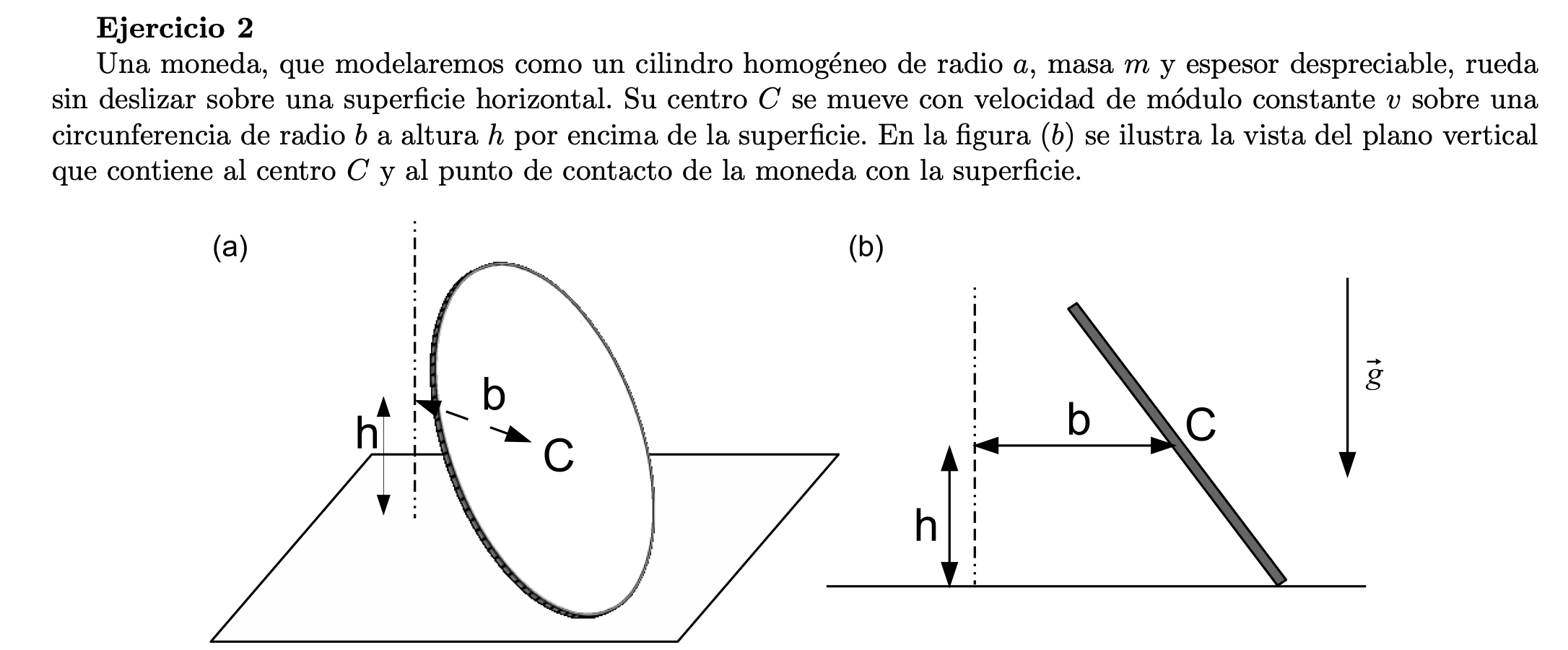
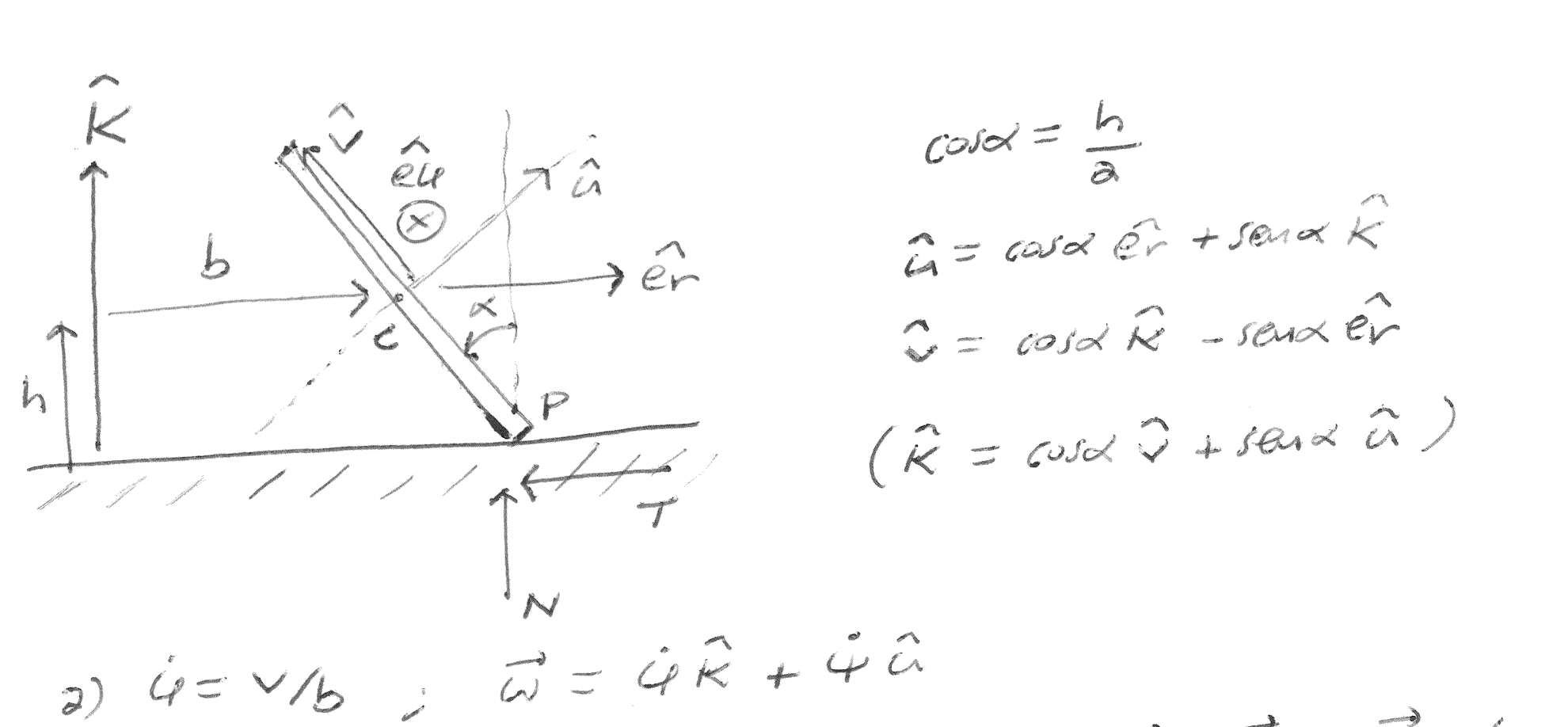
Buenas, tenía una duda de por qué en la solución plantearon la condición de rodadura sin deslizar con el movimiento que hace la moneda con respecto al eje K y no con la rotación de la moneda con el eje u, es decir que v= (dΨ/dt) x a
gracias



Bien, ahora está más encaminado.
Te está faltando observar que la moneda es un rígido que rota sobre sí mismo (según 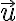 ), pero además está rotando entorno al eje
), pero además está rotando entorno al eje 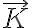 .
.
Con la información que le estás dando a la velocidad angular, estás diciendo que rueda sin deslizar en una trayactoria recta y eso no es así. Hay que aplicar adición de velocidades angulares.
¿Se entiende?