Claro, el polinomio característico tiene raíces complejas. Además, el eje de rotación es un subespacio propio asociado al valor propio 1 y el complemento ortogonal de ese subespacio es un plano que es invariante por la rotación, pero ese subespacio no tiene vectores propios porque "giran 90 grados" al rededor del eje, así que el transformado de un vector en ese plano no es colineal consigo mismo. En resumen no hay más vectores propios que los del eje de rotación, por lo tanto no se puede encontrar una base de vectores propios del espacio.
Una rotación es un operador ortogonal, entonces si hay vectores propios asociados a valores propios distintos, los vectores deben ser ortogonales. Por eso digo que si hay otros vectores propios deben estar en el complemento ortogonal de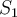
, pero ahí no hay vectores propios.
Espero que no sea demasiado confuso. Por cualquier duda vuelve a consultar.
Una rotación es un operador ortogonal, entonces si hay vectores propios asociados a valores propios distintos, los vectores deben ser ortogonales. Por eso digo que si hay otros vectores propios deben estar en el complemento ortogonal de
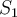, pero ahí no hay vectores propios. Espero que no sea demasiado confuso. Por cualquier duda vuelve a consultar.