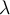Hola Andrés.
Si te fijas en la opción C, que 0 sea val. propio de T equivale a que existe una matriz A 2x2 no nula tal que  .
.
Esto es,  , y como la igualdad tiene que valer para cualquier i, j =1,2, llegamos a 4 ecuaciones de las que se deduce que todos los
, y como la igualdad tiene que valer para cualquier i, j =1,2, llegamos a 4 ecuaciones de las que se deduce que todos los 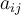 deben ser 0.
deben ser 0.
Entonces no existe una matriz A no nula tal que  por lo que 0 no es valor propio, cualquiera sea el valor de k.
por lo que 0 no es valor propio, cualquiera sea el valor de k.
Por tanto la opción C es verdadera.
Saludos
J.