
Hola buenas noches, para la opción a, busque una base de x+y-z=0, {(1,0,1), (0,1,1)} luego busque su base ortonormal y me dio {(1,0,1) (-1/2,1,1/2)}, cuando sustituyo en la fórmula de ps no llego al resultado. Muchas gracias Saludos

Hola buenas noches, para la opción a, busque una base de x+y-z=0, {(1,0,1), (0,1,1)} luego busque su base ortonormal y me dio {(1,0,1) (-1/2,1,1/2)}, cuando sustituyo en la fórmula de ps no llego al resultado. Muchas gracias Saludos
 (supongo que el producto interno es el usual, si no dice lo contrario). Entonces tenés que tener cuidado de cuál es la fórmula que utilizas. Si
(supongo que el producto interno es el usual, si no dice lo contrario). Entonces tenés que tener cuidado de cuál es la fórmula que utilizas. Si  es una base
es una base  de un subespacio
de un subespacio 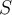 , entonces la proyección ortogonal sobre
, entonces la proyección ortogonal sobre 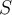 es
es  . Si la base es ortonormal, podés omitir los denominadores ya que
. Si la base es ortonormal, podés omitir los denominadores ya que  para todo
para todo  , pero si no, no. Tal vez ese es el error.
, pero si no, no. Tal vez ese es el error.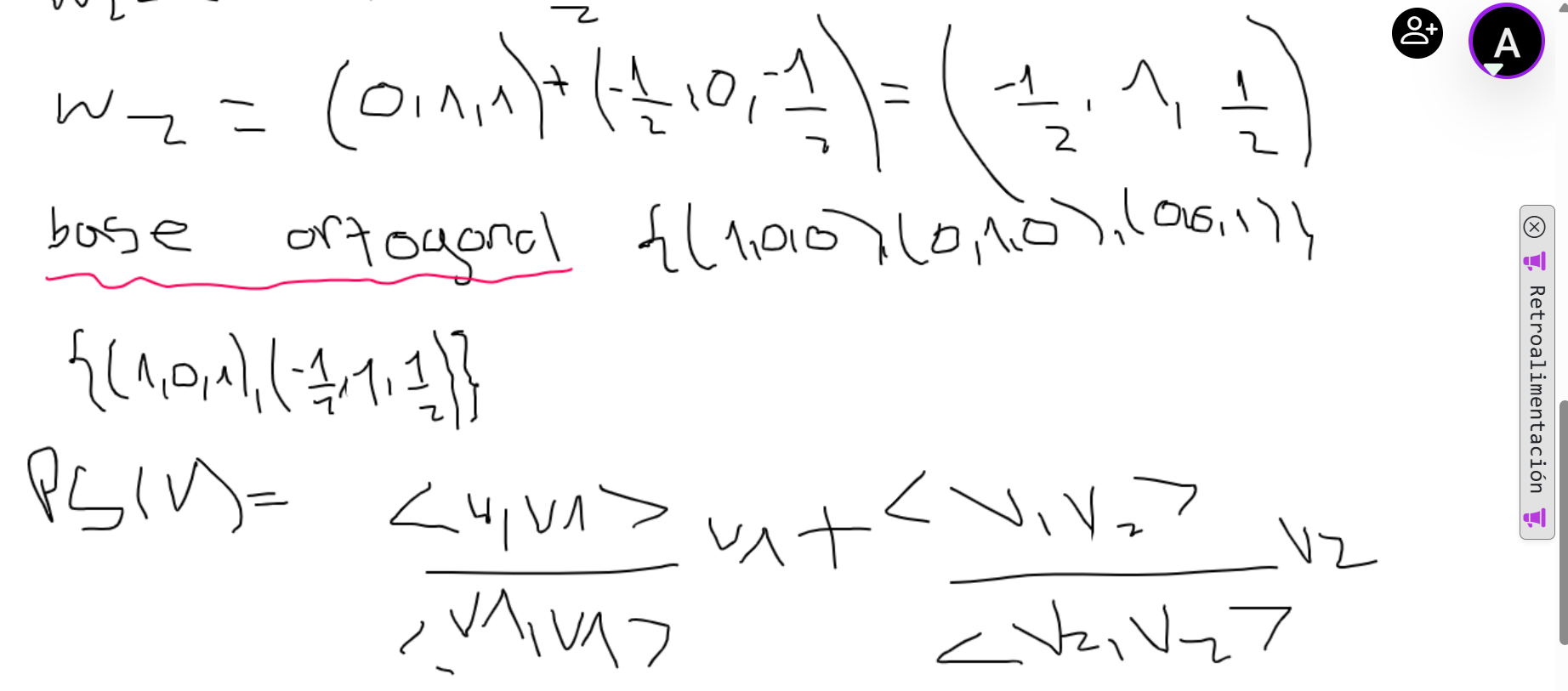
Hola buenas noches muchas gracias por contestar, yo ahora creo que tengo que hacer ps en la base canónica, pero mi base ortogonal tiene dim 2 y la base canónica de (x,y,z )tiene dim 3, no sabria como continuarlo. Saludos
Hola Agustina.
Si S es un SEV de dimensión 2 y P_S(v) es la proyección ortogonal de v sobre S, entonces está bien que P_S(v) sea CL de la base de S.
Saludos
J.


Hola buenas tardes, gracias por la respuesta, hice el ejercicio de nuevo y sigo sin llegar a la solución que muestra, ¿hay algo que este aplicando mal? disculpe las molestias que sigo trancada en este ejercicio. Saludos
Hola Agustina, cuando calculas w2 te equivocas en numerador <v2,w1> ya que w1 no es (1,0,0).
Saludos
J.