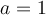Buenas, no entiendo la solución al siguiente ejercicio:


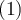 Sé que
Sé que 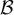 no es
no es  de
de 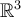 pero no entiendo el hecho de por qué plantear
pero no entiendo el hecho de por qué plantear  donde
donde 
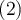 Llegué a la misma
Llegué a la misma  pero no entiendo cómo es que se deduce que
pero no entiendo cómo es que se deduce que  es
es  si y sólo si
si y sólo si  ¿De dónde sale ese polinomio (evaluación)?
¿De dónde sale ese polinomio (evaluación)?