
Hola buenas noches no sabría como plantear este ejercicio para definir ese tipo de respuestas. Muchas gracias

Hola buenas noches no sabría como plantear este ejercicio para definir ese tipo de respuestas. Muchas gracias
Hola Andrés.
Si te fijas en la opción C, que 0 sea val. propio de T equivale a que existe una matriz A 2x2 no nula tal que  .
.
Esto es,  , y como la igualdad tiene que valer para cualquier i, j =1,2, llegamos a 4 ecuaciones de las que se deduce que todos los
, y como la igualdad tiene que valer para cualquier i, j =1,2, llegamos a 4 ecuaciones de las que se deduce que todos los 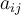 deben ser 0.
deben ser 0.
Entonces no existe una matriz A no nula tal que  por lo que 0 no es valor propio, cualquiera sea el valor de k.
por lo que 0 no es valor propio, cualquiera sea el valor de k.
Por tanto la opción C es verdadera.
Saludos
J.
Hola de nuevo, revisando las cuentas me equivoqué en mi respuesta anterior, en el sistema de ecuaciones la matriz queda no invertible por lo que admite soluciones no triviales, por tanto no es la opción C.
Disculpas y saludos.
J.
