Campo electrico entre dos placas paralelas

Campo electrico entre dos placas paralelas

de Juan Pablo Sierra Ansuas -
Número de respuestas: 1

¿Alguien se anima a explicarme por qué el campo entre dos placas paralelas con cargas +Q y -Q es de la siguiente forma?

\vec{E} = \displaystyle \frac{\sigma}{\epsilon_0} \hat{n}

Más específicamente cómo se deduce a partir de la ley de Gauss y eso.


Gracias!
En respuesta a Juan Pablo Sierra Ansuas

Re: Campo electrico entre dos placas paralelas

de Federico Mario Silva Abramo -

Hola,

te tenés que tomar una superficie gaussiana. Eligiendo el cilindro, "colocamos" una cara del cilindro dentro de la placa conductora (donde no hay campo), y la otra cara fuera. Por la ley de Gauss, el campo que atraviesa al cilindro es igual a la carga encerrada por éste. Además, como el campo es parelelo a las placas laterales del cilindro, el producto interno entre el campo y el vector 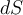dS es cero (suponemos lejos de los bordes). La distribución de la carga en las paredes de la placa es sobre un lado de la placa, el otro lado se mantiene inalterado (esto es porque las cargas entre placas paralelas de distinto signo se atraen). De esta manera, queda:

E\pi r^2=\frac{Q}{\epsilon_0}


Reescribiendo a Q con la densidad de carga (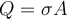 Q=\sigma A donde A es el área de la porción de placa), llegamos a que

E=\frac{\sigma}{\epsilon_0}

Espero haber sido claro,

saludos