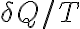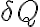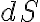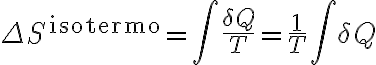Hola Alexis, buenas tardes.
Lo que estás integrando es la expresión que está dentro del argumento de la integral:
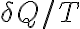
Imagina un proceso termodinámico en el cual se cambia una pequeña cantidad de calor
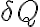
a una cierta temperatura local de intercambio de calor T, entonces tu variación de entropía
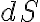
en dicho proceso es el cociente entre ambas magnitudes.
En el caso en particular en que tenés un proceso internamente reversible e isotermo, como en todo momento se mantiene la temperatura constante, la temperatura del denominador sale de la integral:
Esta última integral es la suma total de todos los calores intercambiados durante el proceso, o sea, el calor total.
Un detalle es que, al igual que en la primera ley de la termodinámica, la segunda ley depende de la frontera que definamos para el sistema. En esta definición podemos tomar ventaja de cómo es será la temperatura T que aparece en el denominador, pudiendo hacer más sencillo el cálculo. Esto se debe a que nos interesa saber (para el cálculo) la temperatura local de la frontera del sistema donde se da la transferencia de calor con el ambiente.
Saludos,
m
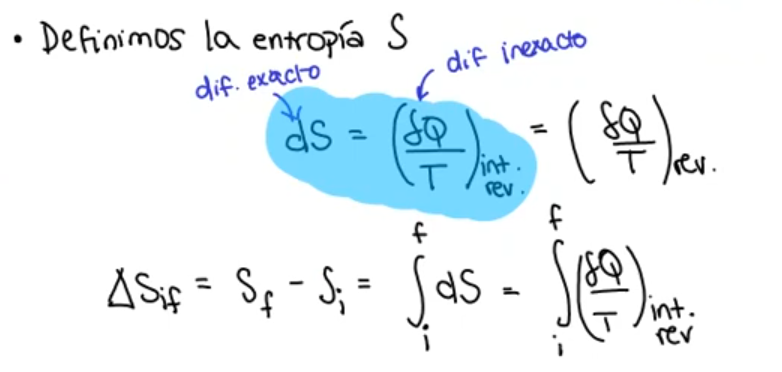
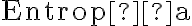 como
como  al momento de calcular
al momento de calcular  ¿Estamos integrando respecto a un
¿Estamos integrando respecto a un 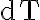 o respecto a qué diferencial hace referencia la segunda integral? ¿Puede que dependiendo del proceso te quede al final
o respecto a qué diferencial hace referencia la segunda integral? ¿Puede que dependiendo del proceso te quede al final 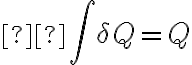 (TFC)?
(TFC)?