Buenas tardes, quería consultar si el procedimiento que hice es correcto, ya que no estoy llegando a la solución. Tengo entendido que en cualquier tipo de proceso, la ecuación de estado es aplicable.
Hola Romano, buenas tardes. Un par de comentarios:
a) Si bien es correcto que la temperatura inicial del aire es de 36 grados Celsius, esto es porque es el aire que el buzo expele (y que se encuentra a dicha temperatura). Esto te lo comento por el hecho de que no es que se mantiene constante la temperatura porque el proceso es adiabático. De hecho, como ya hemos estado viendo en estas semanas, en los procesos adiabáticos el calor intercambiado es nulo pero la temperatura varía durante los mismos. Es decir, ausencia de calor no implica que la temperatura se mantenga constante.
b) Me parece que te estás olvidando de sumar la presión atmosférica (en la superficie del lago) cuando querés hallar la presión en el fondo. Recordá que para un fluido en reposo (como en el lago en este caso), la presión a una cierta profundidad es la presión atmosférica más el peso de la columna de agua a dicha profundidad.
Saludos,
m
a) Si bien es correcto que la temperatura inicial del aire es de 36 grados Celsius, esto es porque es el aire que el buzo expele (y que se encuentra a dicha temperatura). Esto te lo comento por el hecho de que no es que se mantiene constante la temperatura porque el proceso es adiabático. De hecho, como ya hemos estado viendo en estas semanas, en los procesos adiabáticos el calor intercambiado es nulo pero la temperatura varía durante los mismos. Es decir, ausencia de calor no implica que la temperatura se mantenga constante.
b) Me parece que te estás olvidando de sumar la presión atmosférica (en la superficie del lago) cuando querés hallar la presión en el fondo. Recordá que para un fluido en reposo (como en el lago en este caso), la presión a una cierta profundidad es la presión atmosférica más el peso de la columna de agua a dicha profundidad.
Saludos,
m
Buenas tardes, hice la corrección de la presión en el lago, pero sigue sin darme el valor de la solución.
Buenas, yo lo hice usando la constante de los procesos adiabáticos PV^g = cte. y me dio bien. En la parte C) igual no me esta dando.
Me queda el W=-Ctexgxln(Vf/Vi) y da diferente al resultado
Me queda el W=-Ctexgxln(Vf/Vi) y da diferente al resultado
Vi que me equivoqué y era con 1-/g-1 (PfVf-PiVi) pero tampoco me dió
Hola. Demoré en responderles porque estaba discutiendo internamente este ejercicio. Les explico por qué.
Según lo entiendo, la diferencia entre un proceso cuasiestático y no cuasiestático está básicamente en el tiempo en el que transcurre dicho proceso. Si un proceso es "rápido" o "muy rápido", entonces es muy difícil de sostener la hipótesis de cuasiestático. Por otro lado, aquellos procesos que modelamos como muy lentos decimos que son cuasiestáticos. No es sencillo llenar lo que ocurre en el medio, por lo que es un gran problema de ingeniería: cómo modelar y cómo verificar.
Desde mi punto de vista, y bajo el argumento anterior, este proceso no es cuasiestático. Mi argumento es que el tiempo en que se desarrolla el proceso (la burbuja sube "rápido") es suficientemento rápido tal que es posible modelarlo como adiabático (al ser muy rápido, no hay transferencia de calor desde la burbuja al lago), haciendo que además sea no cuasiestático. Bajo esto último, entonces no es posible utilizar la relación que proponen: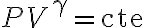
. La solución propuesta utiliza esto y considero que es un modelado erróneo.
Mi propuesta es que al suponer que es un proceso adiabático, pueden hallar el trabajo ocurrido mediante la aplicación de la primera ley, ya que tienen definidos los estados iniciales y finales, además de que saben que la variación de energía interna es una variable de estado, donde su valor no depende de la trayectoria termodinámica que el sistema haya tomado.
Saludos,
m
Según lo entiendo, la diferencia entre un proceso cuasiestático y no cuasiestático está básicamente en el tiempo en el que transcurre dicho proceso. Si un proceso es "rápido" o "muy rápido", entonces es muy difícil de sostener la hipótesis de cuasiestático. Por otro lado, aquellos procesos que modelamos como muy lentos decimos que son cuasiestáticos. No es sencillo llenar lo que ocurre en el medio, por lo que es un gran problema de ingeniería: cómo modelar y cómo verificar.
Desde mi punto de vista, y bajo el argumento anterior, este proceso no es cuasiestático. Mi argumento es que el tiempo en que se desarrolla el proceso (la burbuja sube "rápido") es suficientemento rápido tal que es posible modelarlo como adiabático (al ser muy rápido, no hay transferencia de calor desde la burbuja al lago), haciendo que además sea no cuasiestático. Bajo esto último, entonces no es posible utilizar la relación que proponen:
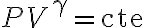. La solución propuesta utiliza esto y considero que es un modelado erróneo.Mi propuesta es que al suponer que es un proceso adiabático, pueden hallar el trabajo ocurrido mediante la aplicación de la primera ley, ya que tienen definidos los estados iniciales y finales, además de que saben que la variación de energía interna es una variable de estado, donde su valor no depende de la trayectoria termodinámica que el sistema haya tomado.
Saludos,
m
Buenas, espero se encuentren bien.
Quería comentarles que ayer consulté con dos colegas del curso de Física Térmica (los profesores Vallejo y Bove) sobre esta pregunta. Dio para un intercambio bastante extenso, y que no es trivial de resolver (para que vean la complejidad del modelado de este problema). Las posturas eran dos: por un lado la que les mencioné en el post anterior; y por otro lado, que el proceso es "rápido" pero aún lo podemos modelar como si fuese cuasiestático.
Por simplicidad del asunto, creo que lo más conveniente en este caso es que lo modelen como si fuese cuasiestático (planteando la relación /( PV^\gamma = \text{cte} /) ) para que sea más sencillo de resolver.
Saludos,
m
PD: El argumento de que este proceso es cuasiestático radicaba en el hecho de los tiempos característicos de transferencia de calor y con la experiencia que el docente (Ítalo en este caso) ha tenido en este tema. Me mencionó que realizó experimentos con cohetes de agua, donde hay expansiones muy rápidas que de alguna manera se pueden modelar utilizando lo que hemos visto en el curso (más algunas otras cositas). Luego, entramos en la parte de entropía del universo. Como les mencioné, es un tema que vamos a continuar discutiendo pero no es tan sencillo de resolver.
Quería comentarles que ayer consulté con dos colegas del curso de Física Térmica (los profesores Vallejo y Bove) sobre esta pregunta. Dio para un intercambio bastante extenso, y que no es trivial de resolver (para que vean la complejidad del modelado de este problema). Las posturas eran dos: por un lado la que les mencioné en el post anterior; y por otro lado, que el proceso es "rápido" pero aún lo podemos modelar como si fuese cuasiestático.
Por simplicidad del asunto, creo que lo más conveniente en este caso es que lo modelen como si fuese cuasiestático (planteando la relación /( PV^\gamma = \text{cte} /) ) para que sea más sencillo de resolver.
Saludos,
m
PD: El argumento de que este proceso es cuasiestático radicaba en el hecho de los tiempos característicos de transferencia de calor y con la experiencia que el docente (Ítalo en este caso) ha tenido en este tema. Me mencionó que realizó experimentos con cohetes de agua, donde hay expansiones muy rápidas que de alguna manera se pueden modelar utilizando lo que hemos visto en el curso (más algunas otras cositas). Luego, entramos en la parte de entropía del universo. Como les mencioné, es un tema que vamos a continuar discutiendo pero no es tan sencillo de resolver.