Consultas del libro de ejercicio - Capítulo 7: Cálculo de integrales

Buenas

Primero debemos entender como es la figura

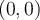Por ejemplo el circulo de radio $1$ y centro $(0,0)$ es es el conjunto $\{(x,y) \in \mathbb{R}^{2} : x^{2} + y^{2} \leq 1\}$ y en ese caso podemos plantear el área como la integral $\displaystyle \int_{-1}^{1} \sqrt{1 - x^{2}} - \left(-\sqrt{1-x^2}\right) dx$ donde $\sqrt{1 - x^{2}}$ y $(-\sqrt{1-x^2})$ son las funciones que delimitan la región.

En el ejercicio que mencionas, primero hay que mencionar que tanto $x$ como $y$ tienen que ser mayor igual a 0, y también deben ser menor o igual que 9. Luego puedes expresar $y$ como una funcion de $x$, mas preciamente $y \leq (3-\sqrt{x})^2$.

Por lo tanto el área en este caso es $\displaystyle \int_{0}^{9} (3-\sqrt{x})^{2} dx$

Agrego una imagen de la figura

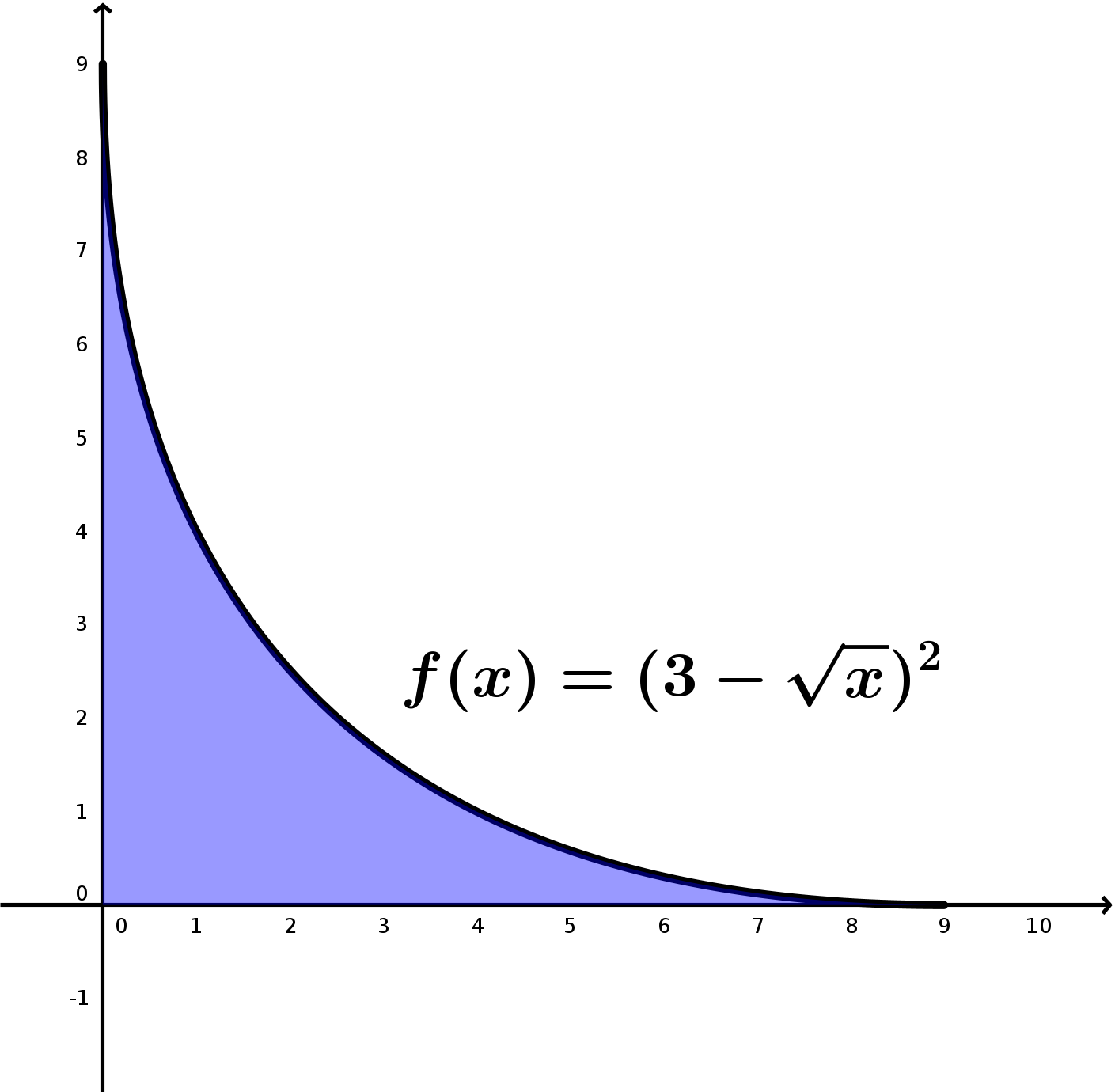
Saludos