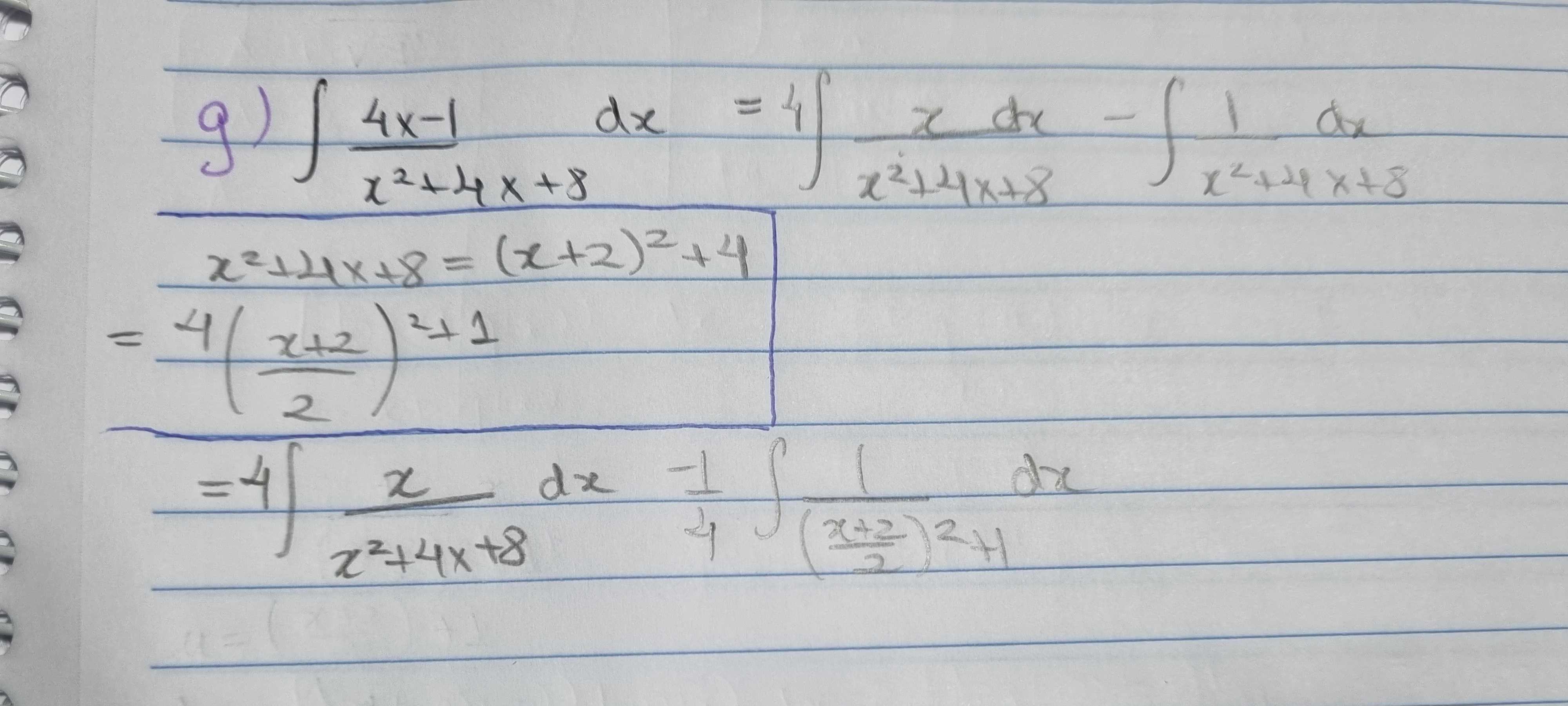7.2 ej 3 parte g

7.2 ej 3 parte g

de Delfina Bovio Amorin -
Número de respuestas: 4

Buenas tardes, intenté resolver esta integral separándola en dos sumandos pero no entiendo como se puede calcular la integral de x entre un polinomio de segundo grado sin raíces reales. O quizás se pueda resolver por otro método.

Adjunto 1000089578.jpg
En respuesta a Delfina Bovio Amorin

Re: 7.2 ej 3 parte g

de Marcos Barrios -

Buenas

Si bien el ejercicio dice aplicando fracciones simples, un poco de cambio de variable hay que usar (cambios lineales o cuadraticos).

Cuando tienes un problema como el que mencionas, una idea es llevar el denominador a x^{2} + 1, ya que

\displaystyle \int_{a}^{b} \frac{\alpha x + \beta}{x^{2} + 1} dx = \int_{a}^{b} \frac{\alpha x dx}{x^{2}+1} + \int_{a}^{b} \frac{\beta dx}{x^{2} + 1}

En ese caso la primer integral la puedes calcular con el cambio de variable x^{2} = t mientras que para la segunda debes recordar que una primitiva de \frac{1}{x^{2}+1} es \arctan. En resumen

\displaystyle \int_{a}^{b} \frac{\alpha x + \beta}{x^{2} + 1} dx = \frac{\alpha}{2}\log(x^{2} + 1) \vert_{a}^{b} + \beta \arctan(x) \vert_{a}^{b}

La pregunta ahora es como llevar el denominador a x^{2} + 1

Bien en este caso y como tu realizas en una parte

\displaystyle \frac{4x-1}{x^2 + 4x + 8} = \frac{4x -1}{(x+2)^2 + 4} = \frac{1}{4} \times \frac{4x - 1}{\left( \frac{x+2}{2}\right)^{2} + 1 }

Realizando el cambio \frac{x+2}{2} = t tenemos

\displaystyle \int \frac{4x-1}{x^2 + 4x + 8} dx = \int \frac{1}{4} \times \frac{8t -8 - 1 }{t^{2} + 1} 2dt

Tenemos asi una integral como la que mencione antes

Ten en cuenta de deshacer el cambio de variable sobre el final

Cualquier cosa vuelve a escribir

Saludos
En respuesta a Marcos Barrios

Re: 7.2 ej 3 parte g

de Julieta Recoba Argul -

Buenas, con respecto a este ejercicio, entiendo como hacer la parte del arcotangente pero no me sale la primera primitiva(la que tiene en el numerador 4x). Cuando hago el cambio de variable  nose que hacer con la variable que me queda en el numerador.

ejercicio 7.3.3 parte g)

En respuesta a Julieta Recoba Argul

Re: 7.2 ej 3 parte g

de Marcos Barrios -

Buenas

En general te conviene primero pasar el denominador a la expresión con 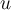u, pero veamos tus pasos

Cuando realizas el cambio u = \frac{x+2}{2}, la integral el segundo sumando queda

\displaystyle \int \frac{1}{4\left( \left( \frac{x+2}{2}\right)^2 +1 \right)} dx = \int \frac{1}{4(u^2 + 1)} 2du

Es decir que falta una contante, pero efectivamente tendrás un múltiplo de arcotangente como primitiva.

Luego el otro sumando cuando realizas el cambio u = \frac{x-2}{2},

\displaystyle \int \frac{4x}{4\left( \left( \frac{x+2}{2}\right)^2 +1 \right)} dx = \int \frac{2u-2}{(u^2 + 1)} 2du = 2\int \frac{2u}{u^{2} + 1}du - 4 \int \frac{1}{u^{2}+1}

Habia un error en las constantes cuando operaste con el cambio de variable. El segundo termino es igual que el caso anterior

Para el primero debes recordar que hay una primitiva concreta en este tipo de funciones, mas en concreto

\displaystyle \int \frac{2u}{u^{2} + 1} du = \log(u^2 +1)

Puedes resolver esa integral con el cambio de variable t = u^2 + 1

También puedes repasar las primeras primitivas con las que trabajamos (ejercicio 7.1-15)

Te pido disculpas por la demora en responder ya que se nos paso el mensaje

Saludos