EJ 2

EJ 2

de Alexis Sokorov Vargas -
Número de respuestas: 2

Buenas, me gustaría saber si el procedimiento es correcto para el ejercicio:

Primero comprobé que las columnas de la matriz sean una BON de 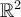\mathbb{R}^2 y luego hice lo siguiente:


\chi_T (\lambda) = (\lambda - 1 )(\lambda + 1) \Rightarrow \lambda _1 = 1 ; \thinspace \lambda _2 = -1


Quedándome S_1 = \{(x,y) \in \mathbb{R}^2 : -2x-y=0\} con \{ (1,-2) \} \xrightarrow{b} S_1 ; S_{-1} = \{(x,y) \in \mathbb{R}^2 : x-2y=0\} con \{ (\frac{1}{2},1) \} \xrightarrow{b} S_{-1}

  Como \text{det(A)} = -1 \Rightarrow T \thinspace \text{es simetría axial}       

No sé si saber que \text{traza(A)} = 0 me sirva de algo          
En respuesta a Alexis Sokorov Vargas

Re: EJ 2

de Luciano Matias Muñiz Manasliski -
Hola.
Está todo bastante bien. Te falta comentar al principio que que la matriz asociada en la base canónica es justamente esa. Es algo general en realidad si Tv=A.v, entonces la matriz asociada a T en la base canónica es A (no hay problema con eso).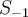
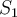Tenés un detalle con la base de S_{-1}, te quedan las coordenadas al revés, debería ser (1,1/2). Una manera de detectar ese tipo de errores es verificando que los vectores de la base de S_1 deben ser ortogonales a los de 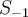S_{-1}; en este caso no te quedaron ortogonales.
Otro par de detalles más: 1. para demostrar que es \textbf{isometría} en realidad es suficiente con ver que es ortogonal, luego si los valores propios son 1 y -1 (\det T=-1) es una \textbf{simetría}, axial en este caso.
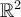2. Lo que hiciste para comprobar que es ortogonal está bien, pero también podés hacer lo que dijiste al principio: que las columnas de la matriz asociada en una base ortonormal queda una base ortonormal de \mathbb{R}^2 y eso es suficiente (que en el fondo es exactamente la misma cuenta que hay que hacer para AA^t=Id).
En este caso la traza=0 te dice que los valores propios son opuestos, pero a eso ya lo habías calculado, así que no te aporta nada. ¿Qué otras posibilidades hay para una matriz ortogonal con traza = 0 , qué valores propios puede tener?